Em direção a uma seleção multivariada eficaz em experimentos biológicos
This post is also available in English
Em nosso artigo recente na Bioinformatics, Maicon Nardino e eu descrevos um novo índice multivariado de distância genótipo-ideótipo, MGIDI, para seleção e recomendação de tratamentos em experimentos biológicos. Então, preparei este breve tutorial sobre a computação do MGIDI.

Motivação
Nardino e eu trabalhamos com dados multivariados desde que comecei meu mestrado na Universidade Federal de Santa Maria (cerca de cinco anos atrás), e selecionar genótipos com base em múltiplas características sempre foi nosso objetivo. Aqui preciso agradecer a todos os integrantes do Laboratório de Melhoramento Genético e Produção de plantas em especial ao meu orientador de Mestrado na época, Velci Queiróz de Souza. Muito obrigado por tudo!
Dados multivariados são comuns em experimentos biológicos e o uso de informação multivariada é crucial para tomar melhores decisões de recomendações de tratamentos ou seleção de genótipos. Índices clássicos para seleção multivariada, como Smith e Hazel estão disponíveis, mas a presença de multicolinearidade e a escolha arbitrária de coeficientes de ponderação podem corroer os ganhos genéticos.
Depois que um dos capítulos de minha tese de doutorado foi publicado como “Mean Performance and Stability in Multi‐Environment Trials II: Selection Based on Multiple Traits” estava convencido de que combinar princípios de diferentes técnicas multivariadas seria uma boa estratégia para a criação de um índice multivariado para seleção de genótipos em que a maioria das características são selecionadas favoravelmente. Preciso também agradecer aqui meu orientador de Doutorado, Alessandro Dal’Col Lúcio por todo apoio e parceria e os colegas de Graduação e Pós-graduação na Época. Em 2019 Nardino já era Professor de Genética e Melhoramento da Universidade Federal de Viçosa e eu Professor de Agronomia do Centro Univesitario UNIDEAU. Depois de diversas longas chamadas pelo Skype, tínhamos os fundamentos teóricos do índice MGIDI.
Fundamentos teóricos
A teoria por trás do índice MGIDI é centrada em quatro etapas principais.
-
Reescalar as variáveis para que todas tenham um intervalo de 0-100.
-
Usar uma análise fatorial para considerar a estrutura de correlação entre as variáveis e redução de dimensionalidade dos dados.
-
Planejar um ideótipo com base em valores conhecidos/desejados de características.
-
Calcular a distância entre cada genótipo para o ideótipo planejado.
O genótipo/tratamento com o menor MGIDI está então mais próximo do ideótipo e, portanto, apresenta os valores mais desejados para todas as características em estudo.
Implementação em software
O pacote R
metan está sendo reconhecido e utilizado entre melhoristas, principalmente. Portanto, parecia lógico que não havia outra maneira de providenciar acesso livre e de código aberto ao índice MGIDI do que implementá-lo no
metan. E aqui estamos! o índice MGIDI pode ser computado com metan::mgidi().
A última versão estável do metan está disponível no
CRAN e pode ser obtida com
# A última versão estável é instalada com
install.packages("metan")
# Ou a versão de desenvolvimento do GitHub:
# install.packages ("devtools")
devtools::install_github("TiagoOlivoto/metan")
Os usuários podem computar o índice usando dados baseados em repetição ou dados baseados em média.
Usando dados baseados em repetições
Quando dados baseados em repetição estão disponíveis, ambos modelos de efeitos mistos ou fixos podem ser ajustados com gamem() e gafem(), respectivamente. Neste exemplo, iremos reproduzir os resultados da seleção do genótipos de trigo realizada em nosso artigo.
A primeira etapa é ajusar o modelo. Neste caso, um modelo de efeito misto com genótipo como efeito aleatório.
library(metan)
# Registered S3 method overwritten by 'GGally':
# method from
# +.gg ggplot2
# |=========================================================|
# | Multi-Environment Trial Analysis (metan) v1.15.0 |
# | Author: Tiago Olivoto |
# | Type 'citation('metan')' to know how to cite metan |
# | Type 'vignette('metan_start')' for a short tutorial |
# | Visit 'https://bit.ly/pkgmetan' for a complete tutorial |
# |=========================================================|
dados <-
read.csv("https://bit.ly/2Z0A7FL", sep = ";") %>%
as_factor(GEN, BLOCK)
# Ajustar o modelo de efeito misto
mod <- gamem(dados,
gen = GEN,
rep = BLOCK,
resp = everything(),
verbose = FALSE)
Após ajustar o modelo misto, nós o usamos como dados de entrada na função mgidi(). Neste caso, nosso objetivo foi selecionar genótipos com ganhos negativos para os primeiros quatro caracteres em dados e ganhos positivos para os últimos 10 caracteres.
mgidi_index <-
mgidi(mod,
ideotype = c(rep("l", 4), rep("h", 10)),
SI = 15,
verbose = FALSE)
gmd(mgidi_index) %>% round_cols()
# Class of the model: mgidi
# Variable extracted: sel_dif
# # A tibble: 14 x 11
# VAR Factor Xo Xs SD SDperc h2 SG SGperc sense goal
# <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
# 1 NSS FA1 15.5 16.0 0.45 2.9 0.77 0.34 2.22 increase 100
# 2 SL FA1 8.63 9.12 0.5 5.78 0.67 0.33 3.86 increase 100
# 3 SW FA1 2.17 2.54 0.37 17.1 0.84 0.31 14.3 increase 100
# 4 NGS FA1 40.5 42.0 1.51 3.73 0.65 0.99 2.45 increase 100
# 5 GMS FA1 1.62 1.88 0.26 16.0 0.81 0.21 13.0 increase 100
# 6 HW FA2 76.3 77.7 1.37 1.79 0.8 1.1 1.44 increase 100
# 7 HIS FA2 74.7 74.2 -0.52 -0.7 0.79 -0.41 -0.55 increase 0
# 8 PH FA3 86.5 86.4 -0.08 -0.09 0.78 -0.06 -0.07 decrease 100
# 9 SH FA3 77.8 77.1 -0.7 -0.9 0.82 -0.57 -0.74 decrease 100
# 10 FLH FA3 60.4 58.7 -1.68 -2.78 0.83 -1.39 -2.29 decrease 100
# 11 FLO FA4 60.4 59.1 -1.34 -2.22 0.92 -1.24 -2.05 decrease 100
# 12 DIS FA4 2.84 3.11 0.27 9.53 0.9 0.24 8.54 increase 100
# 13 NGSP FA4 2.62 2.64 0.02 0.9 0.52 0.01 0.46 increase 100
# 14 GY FA5 4380. 4621. 241. 5.5 0.72 173. 3.96 increase 100
Em seguida, obtemos a classificação genótipo/tratamento com
plot(mgidi_index)
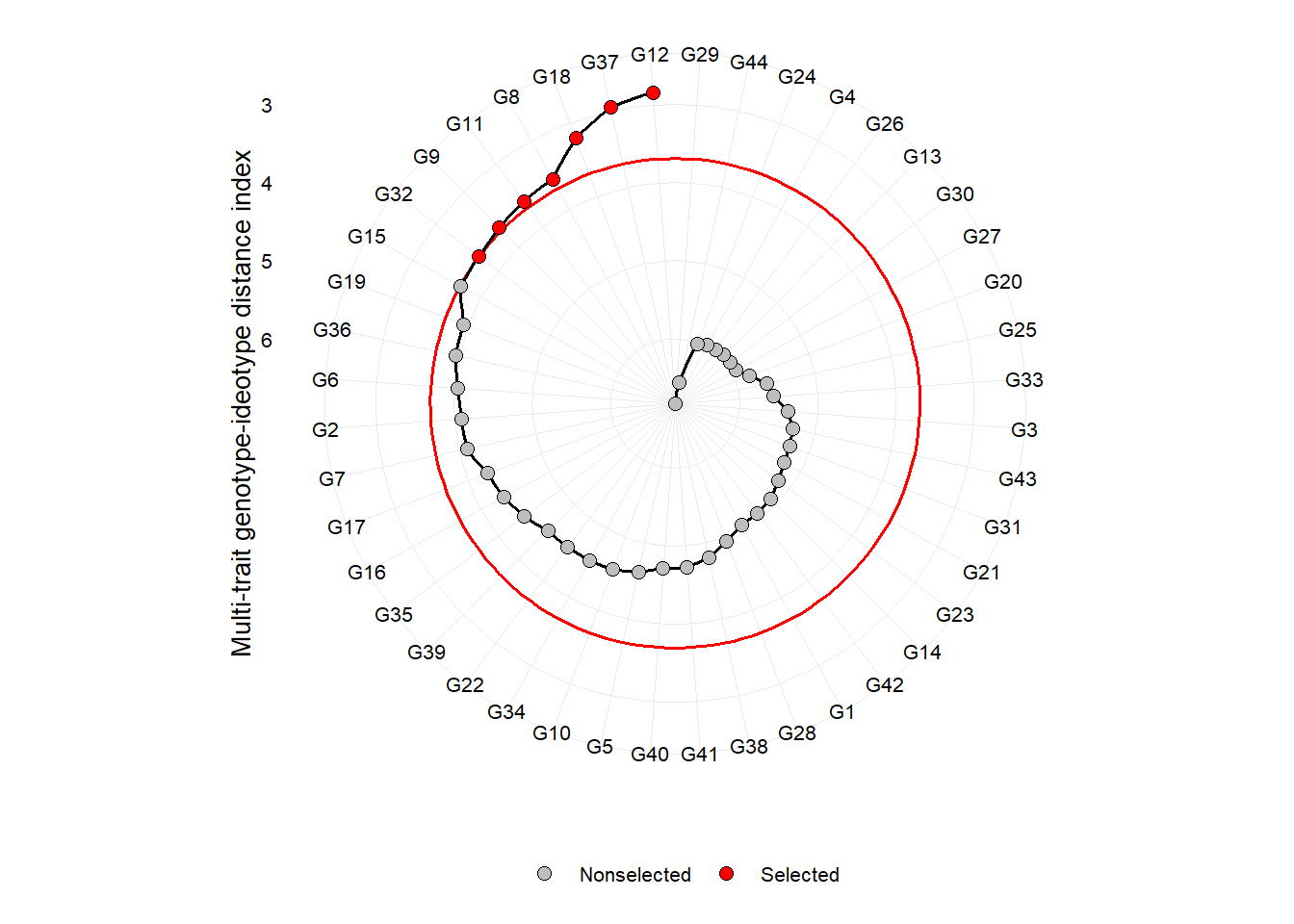
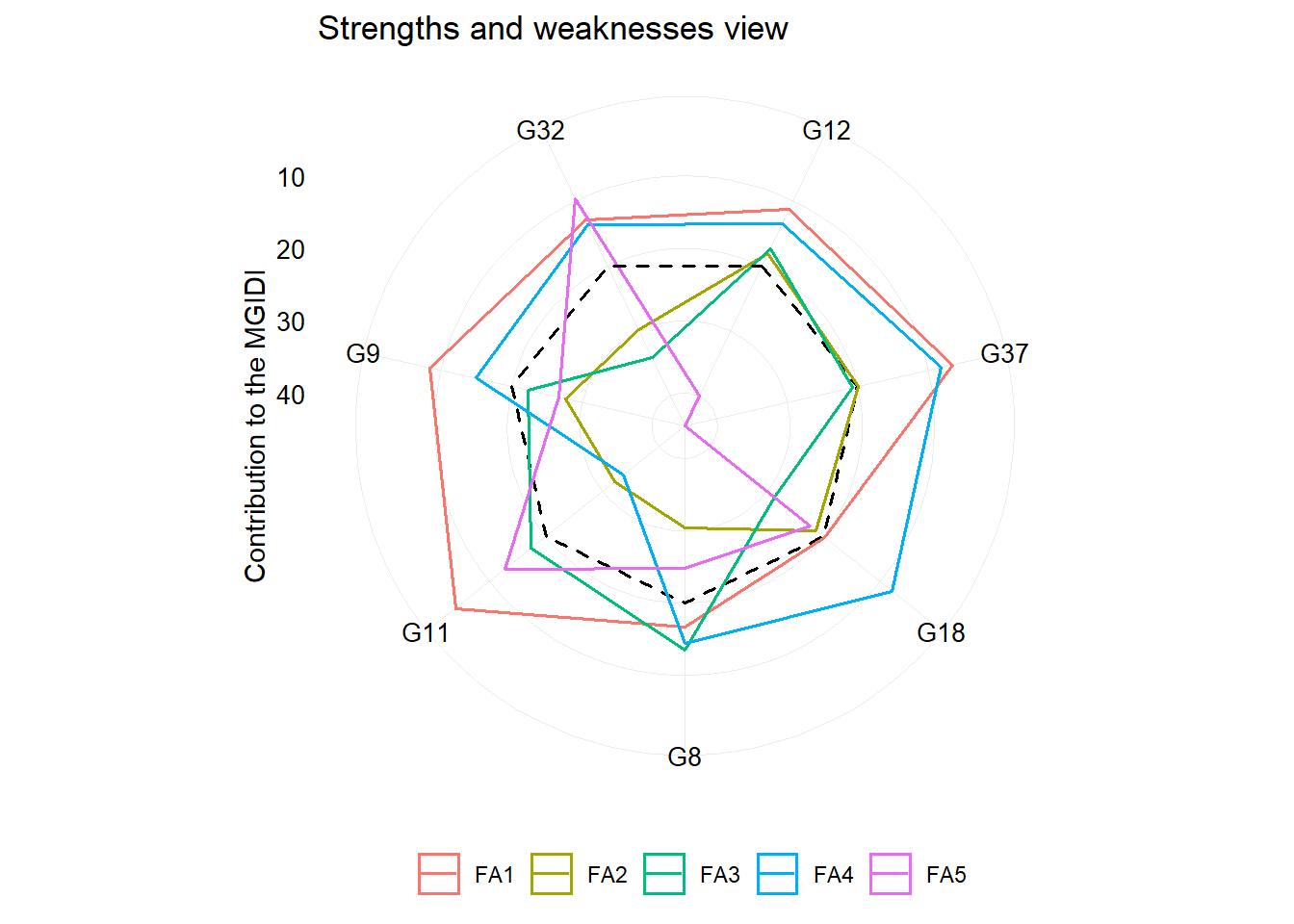
Um dos principais diferenciais do índice MGIDI é a visualização dos pontos fortes e fracos dos genótipos/tratamentos usando o gráfico de radar a seguir. O fator com a menor contribuição estará mais próximo da borda do radar; então, o genótipo que se destaca por esse fator terá pontos fortes relacionados às características desse fator.
plot(mgidi_index, type = "contribution")
Usando uma tabela de dados bidirecional
Nesta seção, extendemos a teoria do índice MGIDI para avaliar um experimento (
Olivoto et al., 2016) com uma estrutura de tratamento fatorial qualitativo-qualitativo. O objetivo é escolher o melhor tratamento (combinação de fatores) que proporciona os valores desejados para a maioria das características avaliadas. Aqui, o objetivo é obter menores valores para P e PL e maiores valores para as demais características. Observe que a entrada necessária na função mgidi() é uma tabela bidirecional com tratamento/genótipos nos nomes das linhas e características nas colunas.
data_ns <- read.csv ("https://bit.ly/3jKx8Jo", sep = ";")
str(data_ns)
# 'data.frame': 8 obs. of 11 variables:
# $ TRAT: chr "WS_100DR" "WS_30T_40DR_30B" "WS_50T_50DR" "WS_50DR_50B" ...
# $ P : num 91.5 96.8 93.5 96.8 103.5 ...
# $ PL : num 0.99 1.14 1.32 1.12 1.31 1.1 1.38 1.29
# $ L : num 93.2 85.2 71.5 86.8 79 ...
# $ TIL : num 3.56 5.48 6.55 4.47 3.53 5.42 5.33 4.42
# $ SSM : num 582 794 702 626 550 ...
# $ GY : num 5301 6459 6079 5697 5485 ...
# $ HW : num 79.2 79.2 79.2 79.5 78.8 ...
# $ W : num 261 264 224 263 270 ...
# $ GLU : num 30.1 29.9 27.9 29.6 27.6 ...
# $ PROT: num 11.8 11.9 12.6 12.6 12.7 ...
data_mat <- column_to_rownames (data_ns, "TRAT")
# Definir o vetor de ideótipo
ide_vect <- c("l", "l", rep ("h", 8))
ide_vect
# [1] "l" "l" "h" "h" "h" "h" "h" "h" "h" "h"
mgidi_data_ns <-
mgidi(data_mat,
ideotype = ide_vect,
verbose = FALSE)
gmd(mgidi_data_ns) %>% round_cols()
# Class of the model: mgidi
# Variable extracted: sel_dif
# # A tibble: 10 x 8
# VAR Factor Xo Xs SD SDperc sense goal
# <chr> <chr> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
# 1 PL FA1 1.21 1.14 -0.07 -5.49 decrease 100
# 2 L FA1 81.7 85.2 3.59 4.4 increase 100
# 3 HW FA1 79.2 79.2 0.03 0.04 increase 100
# 4 GLU FA1 28.7 29.8 1.12 3.91 increase 100
# 5 PROT FA1 12.3 11.9 -0.4 -3.28 increase 0
# 6 P FA2 97.2 96.8 -0.47 -0.48 decrease 100
# 7 W FA2 256. 264. 7.78 3.04 increase 100
# 8 TIL FA3 4.84 5.48 0.64 13.1 increase 100
# 9 SSM FA3 663. 794. 132. 19.9 increase 100
# 10 GY FA3 5941. 6459 518. 8.73 increase 100
O índice MGIDI indicou o tratamento WS_30T_40DR_30B (30% de N no estágio de perfilhamento, 40% de N no estágio de duplo anel e 30% de N no estágio de emborrachamento com uso de enxofre) como o tratamento de melhor desempenho. Este tratamento fornece os valores desejados (valor menor ou maior) para 9 das 10 características analisadas, portanto, a taxa de sucesso, neste caso, foi de 90%.
O MGIDI na prática
O índice MGIDI permite um processo de seleção único e fácil de interpretar. Além de lidar com variáveis colineares, o índice MGIDI não requer o uso de nenhum peso econômico, proporcionando ganhos mais equilibrados. Isso significa que o índice MGIDI pode ajudar melhoristas a garantir ganhos de longo prazo em características primárias (por exemplo, rendimento de grãos) sem comprometer os ganhos genéticos de características secundárias (por exemplo, altura da planta).
Nosso
Material suplementar fornece os códigos utilizados em nosso artigo que podem ser facilmente adaptados em estudos futuros. Outra função útil do pacote metan que pode facilitar a implementação de índices multi-trait em estudos futuros é coincidence_index(),que tornará mais fácil comparar os índices MGIDI, Smith-Hazel e FAI-BLUP em estudos futuros .
Siga nosso
artigo no Research Gate.
Compartilhe este post nas suas redes sociais.
Aproveite o índice MGIDI.