Pacotes

library(tidyverse)  # manipulação de dados
library(metan)
library(lubridate)    # gráfico de radar
library(rio)        # importação/exportação de dados

clima <- import("https://bit.ly/inmet_fred_2020")

# gerar tabelas html
print_tbl <- function(table, digits = 3, n = NULL, ...){
  if(!missing(n)){
    knitr::kable(head(table, n = n), booktabs = TRUE, digits = digits, ...)
  } else{
  knitr::kable(table, booktabs = TRUE, digits = digits, ...)
  }
}

Relação umidade / temperatura

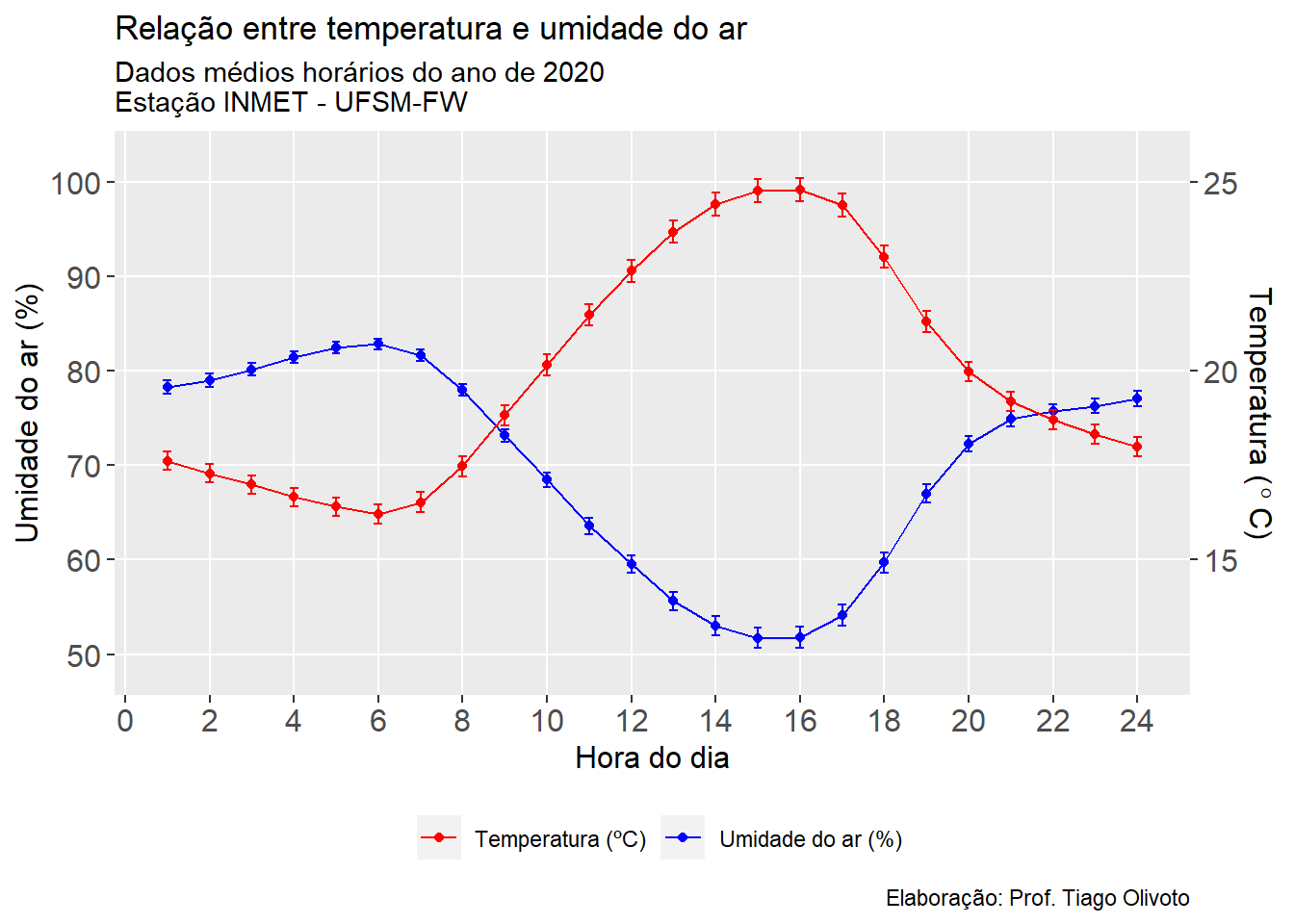
O seguinte gráfico mostra a relação entre umidade e temperatura. Os dados representam a média horária considerando os 366 dias do ano de 2020.

ggplot(clima) + 
  # UMIDADE
  stat_summary(aes(HORA, UM_INST, color = "blue"),
               geom = "point", 
               fun = mean) +
  stat_summary(aes(HORA, UM_INST, color = "blue"),
               geom = "line") + 
  stat_summary(aes(HORA, UM_INST, color = "blue"),
               geom = "errorbar", width = 0.2) +
  # TEMPERATURA
  stat_summary(aes(HORA, TEMP_INST * 400 / 100,
                   color = "red"),
               geom = "point", 
               fun = mean,
               color = "red") +
  stat_summary(aes(HORA, TEMP_INST * 400 / 100,
                   color = "red"),
               geom = "line") + 
  stat_summary(aes(HORA, TEMP_INST * 400 / 100, 
                   color = "red"),
               geom = "errorbar",
               width = 0.2) +
  scale_y_continuous(name = "Umidade do ar (%)",
                     sec.axis = sec_axis(~ .  * 100 / 400 , name = expression("Temperatura ("~degree~"C)")),
                     expand = expansion(c(0.1, 0.1))) +
  scale_color_identity(guide = "legend") +
  scale_color_identity(breaks = c("red", "blue"),
                       labels = c("Temperatura (ºC)",
                                  "Umidade do ar (%)"),
                       guide = "legend") +
  theme(panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        axis.title = element_text(size = 12),
        axis.text = element_text(size = 12)) + 
  scale_x_continuous(breaks = seq(0,24, by = 2)) + 
  labs(title = "Relação entre temperatura e umidade do ar",
       subtitle = "Dados médios horários do ano de 2020\nEstação INMET - UFSM-FW",
       caption = "Elaboração: Prof. Tiago Olivoto",
       x = "Hora do dia")

Variáveis quantificadoras

df_pf <- import("http://bit.ly/inmet_pf_2020")

Utilizando as temperaturas em bulbo seco (Ts ou Tar) e bulbo umido (Tw), as seguintes variáveis podem ser calculadas (Cálculos baseados no material Aula07 - Umidade do Ar, Chuva e Vento Tw (bulbo umido) = 17°C

• Pressão de saturação de vapor considerando a temperatura do bulbo seco (es\(_Ts\))

\[e{s_{Ts}} = 6,108 \times {10^{\frac{{7,5 \times Tar}}{{237,3 + Tar}}}}\]

• Pressão de saturação de vapor (es) considerando a temperatura do bulbo úmido (es\(_Tw\))

\[e{s_{Tw}} = 6,108 \times {10^{\frac{{7,5 \times Tar}}{{237,3 + Tar}}}}\]

• Pessão real do vapor d’água (e)

\[e = e{s_{Tw}} - \gamma \times \left( {Ts - Tw} \right)\]

• Umidade relativa do ar (UR)

\[UR = \frac{e}{{e{s_{Ts}}}} \times 100\]

• Déficit de saturação (\(\delta e\))

\[\Delta e = es - e\]

• Temperatura no ponto de orvalho (T\(o\))

\[{T_o} = \frac{{237,3 \times \log \left( {e/6,108} \right)}}{{7,5 - \log \left( {e/6,108} \right)}}\]

• Umidade absoluta (UA, g vapor m\({-3}\) ar úmido)

\[UA = 216,6 \times \frac{e}{{273 + {T_{ar}}}}\]

• Umidade de saturação (US, g vapor m\({-3}\) ar úmido)

\[UA = 216,6 \times \frac{{e{s_{Ts}}}}{{273 + {T_{ar}}}}\]

• Razão de mistura (r, g vapor / g ar seco). Neste caso, a pressão já consta no enunciado da questão, mas pode ser calculado com a fórmula abaixo (P), onde z é a altitude do local (metros).

\[\begin{array}{l}r = 0,622 \times \frac{e}{{P - e}}~~~~P = 1013,3 \times {\left( {1 - \frac{{0,0065 \times z}}{{293}}} \right)^{5,2568}}\end{array}\]

• Umidade específica (q, g vapor / g ar úmido):

\[q = 0,622 \times \frac{e}{{P - 0,378 \times e}}\]