library(metan)
## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2
## |=========================================================|
## | Multi-Environment Trial Analysis (metan) v1.15.0        |
## | Author: Tiago Olivoto                                   |
## | Type 'citation('metan')' to know how to cite metan      |
## | Type 'vignette('metan_start')' for a short tutorial     |
## | Visit 'https://bit.ly/pkgmetan' for a complete tutorial |
## |=========================================================|
library(rio)
df_ge <- import("http://bit.ly/df_ge", setclass = "tbl")

# gerar tabelas html
print_tbl <- function(table, digits = 3, ...){
  knitr::kable(table, booktabs = TRUE, digits = digits, ...)
}

Desempenho dos genótipos em cada ambiente

A função ge_plot() pode ser usada para visualizar o desempenho do genótipo nos ambientes.

a <- ge_plot(df_ge, ENV, GEN, MMG)
b <- ge_plot(df_ge, ENV, GEN, MMG, type = 2)
arrange_ggplot(a, b, tag_levels = "a")

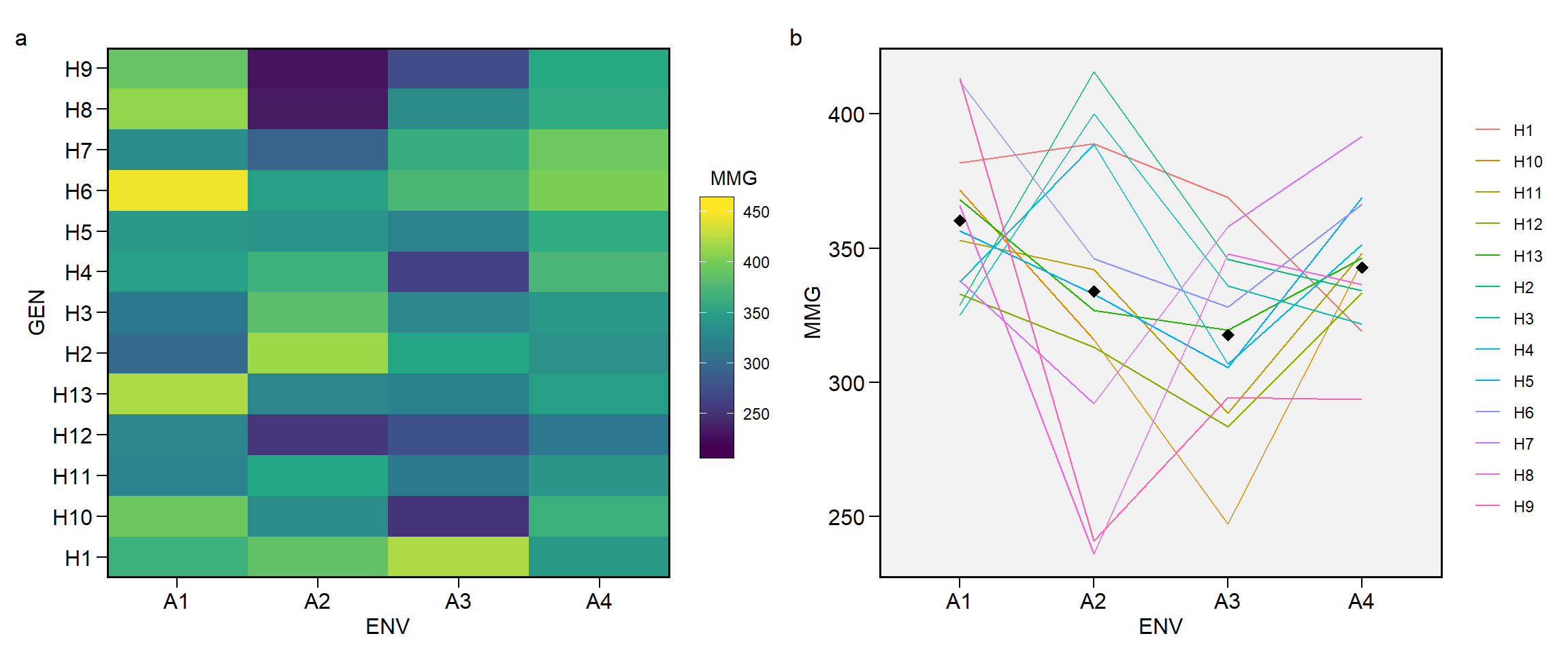
Para identificar o genótipo ganhador em cada ambiente, podemos usar a função ge_winners().

ge_winners(df_ge, ENV, GEN, resp = everything()) %>% print_tbl()

ENV	ALT_PLANT	ALT_ESP	COMPES	DIAMES	COMP_SAB	DIAM_SAB	MGE	NFIL	MMG	NGE
A1	H3	H1	H6	H6	H8	H6	H6	H2	H9	H2
A2	H2	H1	H6	H2	H2	H6	H2	H2	H2	H6
A3	H13	H13	H4	H13	H6	H2	H13	H13	H1	H13
A4	H5	H5	H7	H11	H5	H7	H7	H11	H7	H9

Ou obter a classificação dos genótipos em cada ambiente.

winners <- 
ge_winners(df_ge, ENV, GEN,
           resp = everything(),
           type = "ranks",
           better = c("l, l, h, h, h, h, h, h, h, h"))

print_tbl(winners)

ENV	ALT_PLANT	ALT_ESP	COMPES	DIAMES	COMP_SAB	DIAM_SAB	MGE	NFIL	MMG	NGE
A1	H8	H2	H6	H6	H8	H6	H6	H2	H9	H2
A1	H12	H8	H11	H13	H9	H11	H13	H13	H6	H13
A1	H1	H12	H10	H10	H6	H9	H9	H3	H1	H3
A1	H11	H6	H4	H9	H10	H10	H2	H7	H10	H4
A1	H6	H11	H5	H8	H13	H5	H1	H12	H13	H6
A1	H13	H13	H9	H2	H7	H4	H4	H8	H8	H12
A1	H7	H3	H3	H3	H12	H8	H3	H6	H5	H7
A1	H10	H5	H7	H1	H11	H3	H8	H10	H11	H8
A1	H2	H7	H1	H7	H5	H7	H5	H4	H7	H5
A1	H5	H10	H12	H4	H1	H1	H10	H1	H4	H11
A1	H4	H9	H8	H12	H3	H12	H11	H11	H12	H1
A1	H9	H4	H2	H5	H4	H2	H7	H9	H2	H10
A1	H3	H1	H13	H11	H2	H13	H12	H5	H3	H9
A2	H8	H8	H6	H2	H2	H6	H2	H2	H2	H6
A2	H10	H12	H4	H1	H13	H4	H6	H1	H3	H5
A2	H12	H10	H5	H6	H1	H5	H4	H6	H1	H2
A2	H7	H11	H2	H3	H3	H13	H3	H13	H4	H13
A2	H11	H13	H13	H13	H4	H2	H1	H9	H6	H10
A2	H9	H7	H10	H4	H5	H10	H5	H8	H11	H4
A2	H13	H9	H3	H5	H11	H3	H13	H5	H5	H7
A2	H5	H5	H11	H7	H12	H11	H11	H7	H13	H1
A2	H6	H6	H1	H11	H7	H7	H10	H12	H10	H9
A2	H4	H4	H7	H12	H6	H1	H7	H3	H12	H11
A2	H1	H2	H8	H10	H10	H9	H12	H4	H7	H8
A2	H3	H3	H9	H9	H9	H8	H8	H10	H9	H3
A2	H2	H1	H12	H8	H8	H12	H9	H11	H8	H12
A3	H9	H9	H4	H13	H6	H2	H13	H13	H1	H13
A3	H10	H4	H2	H2	H1	H4	H5	H5	H7	H5
A3	H3	H3	H13	H1	H5	H5	H2	H6	H8	H12
A3	H4	H5	H9	H5	H7	H3	H1	H11	H2	H10
A3	H5	H10	H1	H6	H2	H13	H7	H12	H3	H11
A3	H8	H2	H3	H7	H8	H9	H12	H1	H6	H4
A3	H11	H8	H8	H12	H3	H8	H4	H2	H13	H2
A3	H6	H1	H5	H3	H4	H1	H8	H7	H4	H7
A3	H2	H11	H7	H11	H13	H11	H11	H10	H5	H1
A3	H7	H7	H11	H8	H9	H7	H3	H3	H9	H3
A3	H1	H6	H10	H4	H11	H10	H6	H8	H11	H9
A3	H12	H12	H12	H10	H12	H6	H9	H9	H12	H6
A3	H13	H13	H6	H9	H10	H12	H10	H4	H10	H8
A4	H9	H9	H7	H11	H5	H7	H7	H11	H7	H9
A4	H10	H3	H8	H5	H10	H8	H5	H1	H5	H1
A4	H3	H11	H9	H1	H6	H9	H4	H12	H6	H8
A4	H6	H2	H6	H4	H11	H6	H8	H4	H4	H4
A4	H2	H6	H5	H7	H12	H5	H1	H5	H11	H5
A4	H7	H12	H1	H6	H7	H1	H10	H10	H13	H7
A4	H12	H13	H2	H10	H1	H11	H11	H9	H10	H12
A4	H8	H8	H4	H12	H4	H4	H9	H13	H8	H11
A4	H4	H10	H10	H8	H8	H2	H12	H7	H2	H10
A4	H13	H7	H11	H3	H9	H10	H6	H8	H12	H2
A4	H11	H1	H12	H9	H2	H13	H2	H6	H3	H3
A4	H1	H4	H13	H2	H3	H12	H13	H3	H1	H6
A4	H5	H5	H3	H13	H13	H3	H3	H2	H9	H13

Para mais detalhes sobre os testes, podemos usar ge_details()

details <- ge_details(df_ge, ENV, GEN, resp = everything())
print_tbl(details)

Parameters	ALT_PLANT	ALT_ESP	COMPES	DIAMES	COMP_SAB	DIAM_SAB	MGE	NFIL	MMG	NGE
Mean	2.48	1.34	15.16	49.54	29.01	15.97	172.94	16.12	338.67	511.64
SE	0.03	0.02	0.1	0.22	0.18	0.09	2.62	0.13	3.77	5.82
SD	0.33	0.28	1.25	2.76	2.3	1.17	32.67	1.63	46.91	72.41
CV	13.44	21.16	8.28	5.58	7.95	7.34	18.95	10.16	13.9	14.2
Min	1.71 (H11 in A3)	0.75 (H8 in A2)	11.5 (H3 in A4)	43.48 (H9 in A3)	23.49 (H10 in A3)	12.9 (H3 in A4)	105.72 (H9 in A2)	12.4 (H4 in A3)	218.32 (H9 in A4)	331.8 (H13 in A4)
Max	3.04 (H3 in A1)	1.88 (H1 in A2)	17.94 (H6 in A2)	54.86 (H6 in A1)	34.66 (H8 in A1)	18.56 (H7 in A4)	250.89 (H6 in A1)	21.2 (H2 in A1)	451.68 (H3 in A2)	696.6 (H2 in A1)
MinENV	A3 (2.17)	A3 (1.08)	A3 (14.67)	A3 (47.87)	A3 (28.45)	A3 (15.77)	A3 (146.81)	A3 (15.78)	A3 (317.72)	A3 (467.9)
MaxENV	A1 (2.79)	A1 (1.58)	A1 (15.62)	A1 (51.61)	A1 (29.73)	A1 (16.4)	A1 (199.44)	A1 (16.89)	A1 (360.34)	A1 (557.87)
MinGEN	H10 (2.31)	H8 (1.21)	H12 (14.28)	H9 (47.59)	H12 (28.24)	H12 (14.81)	H9 (152.75)	H9 (15.47)	H9 (310.57)	H3 (491.23)
MaxGEN	H1 (2.62)	H1 (1.5)	H6 (15.76)	H6 (51.53)	H6 (30.25)	H5 (16.59)	H6 (188)	H13 (17.43)	H1 (364.63)	H5 (541.7)

Matriz dupla entrada

A função make_mat() pode ser usada para produzir uma tabela bidirecional com as médias genótipo-ambiente.

mat <- make_mat(df_ge, GEN, ENV, MMG)
print_tbl(mat)

	A1	A2	A3	A4
H1	381.821	388.932	368.768	318.987
H10	371.627	315.936	247.261	345.017
H11	353.036	341.971	288.631	348.023
H12	332.847	313.167	283.633	333.544
H13	368.108	326.857	319.627	346.361
H2	328.861	415.675	345.927	334.220
H3	325.013	400.045	336.053	321.801
H4	337.590	388.658	306.729	351.451
H5	356.492	332.841	305.497	368.845
H6	412.084	346.030	328.038	366.269
H7	338.093	292.069	358.046	391.762
H8	365.720	236.281	347.763	336.371
H9	413.088	241.127	294.359	293.694

Efeitos de interação genótipo-ambiente

A função ge_effects() é usada para calcular os efeitos da interação genótipo-ambiente.

ge_ef <- ge_effects(df_ge, ENV, GEN, MMG)
print_tbl(ge_ef$MMG)

GEN	A1	A2	A3	A4
H1	-4.477	29.157	25.089	-49.769
H10	29.996	0.828	-51.751	20.927
H11	-1.550	13.908	-23.336	10.978
H12	-4.621	2.221	-11.216	13.617
H13	6.199	-8.530	0.337	1.993
H2	-48.980	64.356	10.705	-26.080
H3	-42.386	59.169	11.274	-28.057
H4	-30.187	47.402	-18.430	1.215
H5	-6.097	-3.226	-14.473	23.797
H6	27.308	-12.224	-14.118	-0.966
H7	-28.570	-48.071	34.002	42.640
H8	22.515	-80.401	47.177	10.708
H9	80.850	-64.588	4.740	-21.002

# o mesmo efeito é calculado com o resíduo do modelo aditivo
ge_ef2 <- 
df_ge %>% 
  means_by(GEN, ENV) %>% 
  lm(MMG ~ GEN + ENV, data = .) %>% 
  residuals() %>% 
  matrix(nrow = 13, byrow = TRUE)
print_tbl(ge_ef2)

-4.477	29.157	25.089	-49.769
29.996	0.828	-51.751	20.927
-1.550	13.908	-23.336	10.978
-4.621	2.221	-11.216	13.617
6.199	-8.530	0.337	1.993
-48.980	64.356	10.705	-26.080
-42.386	59.169	11.274	-28.057
-30.187	47.402	-18.430	1.215
-6.097	-3.226	-14.473	23.797
27.308	-12.224	-14.118	-0.966
-28.570	-48.071	34.002	42.640
22.515	-80.401	47.177	10.708
80.850	-64.588	4.740	-21.002

Genótipo + interação genótipo-ambiente (GGE)

Para obter o efeito GGE, usamos argumento type =" gge " na função ge_effects().

gge_ef <- ge_effects(df_ge, ENV, GEN, MMG, type = "gge")
print_tbl(gge_ef$MMG)

GEN	A1	A2	A3	A4
H1	21.484	55.117	51.050	-23.809
H10	11.290	-17.878	-70.457	2.221
H11	-7.301	8.156	-29.087	5.227
H12	-27.489	-20.647	-34.085	-9.251
H13	7.771	-6.958	1.909	3.565
H2	-31.476	81.861	28.209	-8.576
H3	-35.324	66.231	18.336	-20.995
H4	-22.747	54.843	-10.989	8.656
H5	-3.845	-0.974	-12.221	26.049
H6	51.747	12.215	10.320	23.473
H7	-22.244	-41.745	40.328	48.966
H8	5.383	-97.533	30.045	-6.425
H9	52.751	-92.687	-23.359	-49.101

# o mesmo efeito é calculado com o resíduo do modelo aditivo
gge_ef2 <- 
df_ge %>% 
  means_by(GEN, ENV) %>% 
  lm(MMG ~ ENV, data = .) %>% 
  residuals() %>% 
  matrix(nrow = 13, byrow = TRUE)
print_tbl(gge_ef2)

21.484	55.117	51.050	-23.809
11.290	-17.878	-70.457	2.221
-7.301	8.156	-29.087	5.227
-27.489	-20.647	-34.085	-9.251
7.771	-6.958	1.909	3.565
-31.476	81.861	28.209	-8.576
-35.324	66.231	18.336	-20.995
-22.747	54.843	-10.989	8.656
-3.845	-0.974	-12.221	26.049
51.747	12.215	10.320	23.473
-22.244	-41.745	40.328	48.966
5.383	-97.533	30.045	-6.425
52.751	-92.687	-23.359	-49.101

Agrupamento de ambientes

A função ge_cluster() computa uma análise de agrupamento para agrupar ambientes com base em suas semelhanças usando uma distância euclidiana baseada em dados padronizados.

d1 <- ge_cluster(df_ge, ENV, GEN, MMG, nclust = 2)
plot(d1, nclust = 2)

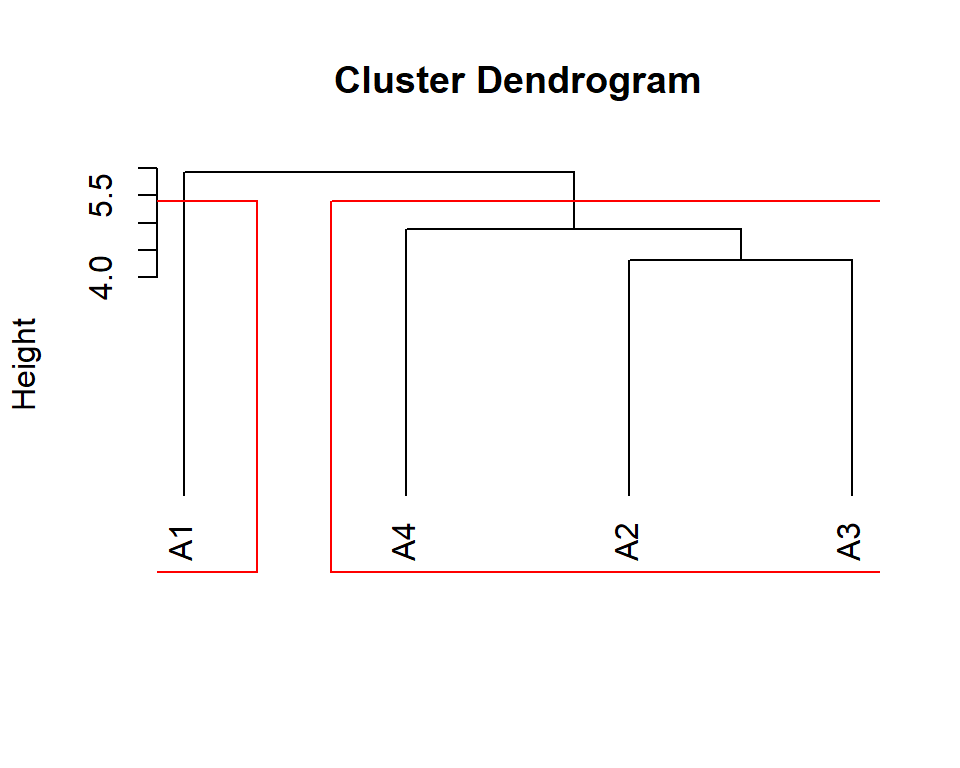
A função env_dissimilarity() calcula a dissimilaridade entre os ambientes de teste usando:

• A partição da partição do quadrado médio da interação genótipo-ambiente (MS_GE) em partes simples (S) e complexas (C), de acordo com Robertson (1959)¹, onde \(S = \frac{1}{2} (\sqrt {Q_1} - \sqrt{Q_2}) ^ 2)\) e \(C = (1-r) \sqrt {Q1-Q2}\), sendo \(r\) a correlação entre a média do genótipo nos dois ambientes; e \(Q_1\) e \(Q_2\) o quadrado médio do genótipo nos ambientes 1 e 2, respectivamente.

• A decomposição do MS_GE proposta por Cruz e Castoldi (1991)² em que a parte complexa é dada por \(C = \sqrt {(1-r) ^ 3 Q1 Q2}\).

• O quadrado médio da interação entre genótipos e pares de ambientes.

• Os coeficientes de correlação entre a média dos genótipos em cada par de ambiente.

mod <- env_dissimilarity(df_ge, ENV, GEN, BLOCO, MMG)
## Evaluating trait Y |=============================================| 100% 00:00:00 

# Coeficiente de correlação de Pearson
print_tbl(mod$MMG$correlation)

	A1	A2	A3	A4
A1	1.000	-0.435	-0.100	-0.234
A2	-0.435	1.000	0.221	0.038
A3	-0.100	0.221	1.000	0.091
A4	-0.234	0.038	0.091	1.000

# Quadrado médio GxEjj '
print_tbl(mod$MMG$MSGE)

	A1	A2	A3	A4
A1	0.000	2723.279	1116.317	901.421
A2	2723.279	0.000	1745.096	1837.028
A3	1116.317	1745.096	0.000	819.735
A4	901.421	1837.028	819.735	0.000

#% Parte simples do QM GxEjj '(Robertson, 1959)
print_tbl(mod$MMG$SPART_RO)

	A1	A2	A3	A4
A1	0.000	13.476	1.203	1.073
A2	13.476	0.000	13.753	26.991
A3	1.203	13.753	0.000	5.600
A4	1.073	26.991	5.600	0.000

#% Da parte complexa do QM  GxEjj '(Robertson, 1959)
print_tbl(mod$MMG$CPART_RO)

	A1	A2	A3	A4
A1	0.000	86.524	98.797	98.927
A2	86.524	0.000	86.247	73.009
A3	98.797	86.247	0.000	94.400
A4	98.927	73.009	94.400	0.000

#% Parte simples do QM  GxEjj '(Cruz e Castoldi, 1991)
print_tbl(mod$MMG$SPART_CC)

	A1	A2	A3	A4
A1	0.000	-3.664	-3.634	-9.882
A2	-3.664	0.000	23.899	28.388
A3	-3.634	23.899	0.000	9.993
A4	-9.882	28.388	9.993	0.000

#% Parte complexa do QM  GxEjj '(Cruz e Castoldi, 1991)
print_tbl(mod$MMG$CPART_CC)

	A1	A2	A3	A4
A1	0.000	103.664	103.634	109.882
A2	103.664	0.000	76.101	71.612
A3	103.634	76.101	0.000	90.007
A4	109.882	71.612	90.007	0.000

Para obter dendrogramas com base na matriz acima, podemos usar plot(). Os dendrogramas são baseados no algoritmo de agrupamento hierárquico UPGMA (método de grupo de pares não ponderados usando médias aritméticas).

plot(mod)

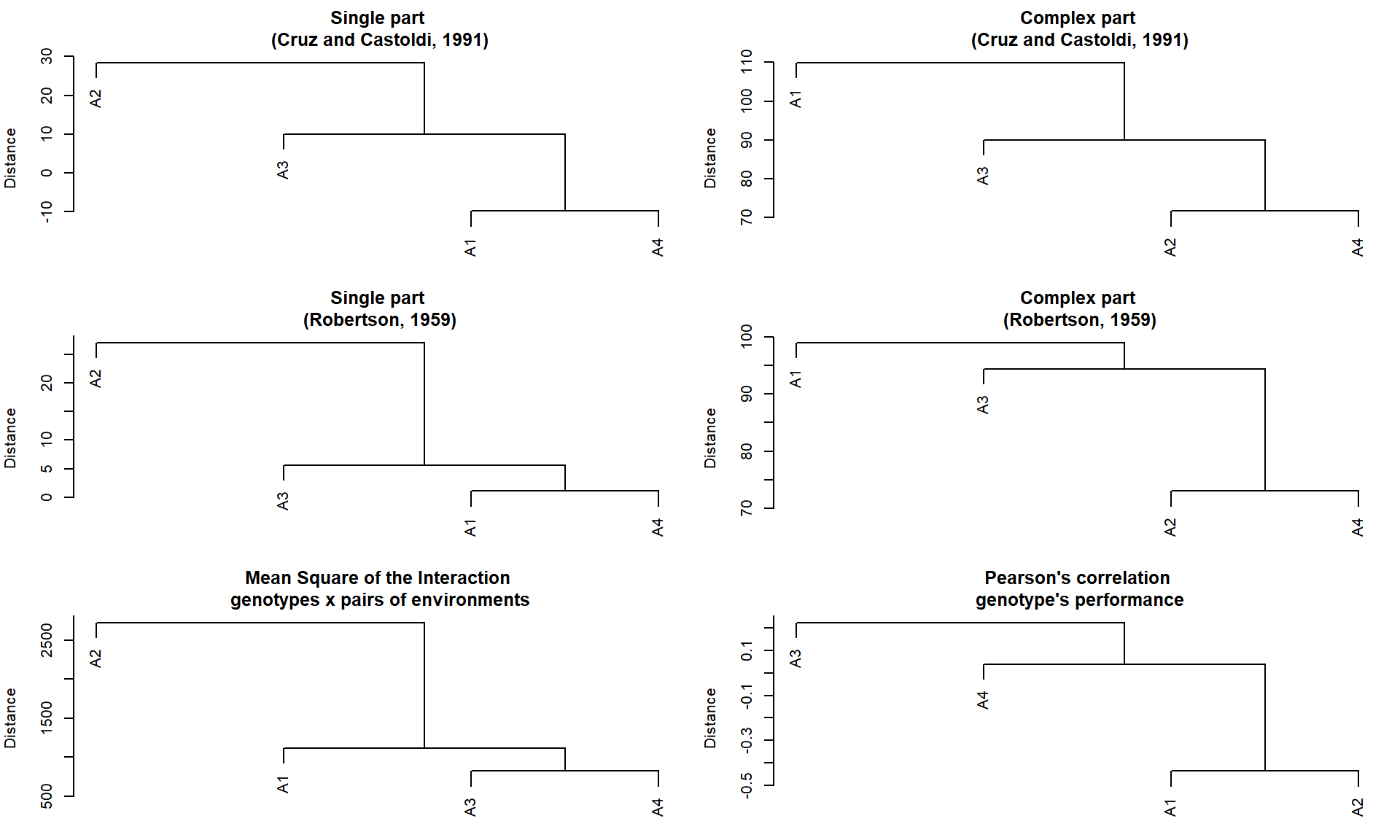
Análise de regressão conjunta

Eberhart e Russell (1966)³ popularizaram a análise de estabilidade baseada em regressão. Neste procedimento, a análise de adaptabilidade e estabilidade é realizada por meio de ajustes de equações de regressão onde a variável dependente é predita em função de um índice ambiental, de acordo com o seguinte modelo:

$$ \mathop Y \nolimits_{ij} = {\beta_{0i}} + {\beta_{1i}}{I_j} + {\delta_{ij}} + {\bar \varepsilon_{ij}} $$

onde \({\beta_{0i}}\) é a média do genótipo \(i\) (\(i\) = 1, 2, …, I); \({\beta_{1i}}\) é a resposta linear (slope) do genótipo \(i\) ao índice ambiental; \(Ij\) é o índice ambiental (\(j\) = 1, 2, …, \(e\)), onde \({I_j} = [(y_{.J} / g) - (y_{..}/ge)]\), \({\delta_{ij}}\) é o desvio da regressão e \({\ bar \varepsilon_{ij}}\) é o erro experimental.

O modelo é ajustado com a função ge_reg(). Os métodos S3 plot() e summary () podem ser usados para explorar o modelo ajustado.

reg_model <- ge_reg(df_ge,
                    env = ENV,
                    gen = GEN,
                    rep = BLOCO,
                    resp = MMG,
                    verbose = FALSE)

# Use o método print()
# ANOVA
print_tbl(reg_model$MMG$anova)

SV	Df	Sum Sq	Mean Sq	F value	Pr(>F)
Total	51	246217.905	4827.802	NA	NA
GEN	12	44633.375	3719.448	0.835	0.616
ENV + (GEN x ENV)	39	201584.529	5168.834	NA	NA
ENV (linear)	1	37012.734	37012.734	NA	NA
GEN x ENV (linear)	12	48764.695	4063.725	0.912	0.548
Pooled deviation	26	115807.101	4454.119	NA	NA
H1	2	8958.150	4479.075	4.877	0.010
H10	2	1618.745	809.372	0.881	0.418
H11	2	1989.689	994.844	1.083	0.343
H12	2	909.811	454.905	0.495	0.611
H13	2	246.901	123.450	0.134	0.874
H2	2	12810.743	6405.372	6.974	0.001
H3	2	10966.021	5483.011	5.970	0.004
H4	2	9729.718	4864.859	5.297	0.007
H5	2	2213.292	1106.646	1.205	0.304
H6	2	476.107	238.053	0.259	0.772
H7	2	15616.320	7808.160	8.502	0.000
H8	2	27920.883	13960.442	15.200	0.000
H9	2	22350.721	11175.360	12.168	0.000
Pooled error	96	88170.644	918.444	NA	NA

# REGRESSÃO
print_tbl(reg_model$MMG$regression)

GEN	b0	b1	t(b1=1)	pval_t	s2di	F(s2di=0)	pval_f	RMSE	R2
H1	364.627	-0.022	-1.7987545	0.0751999942	1186.877	4.877	0.010	27.322	0.000
H10	319.960	2.914	3.3700371	0.0010837020	-36.357	0.881	0.418	11.614	0.937
H11	332.915	1.456	0.8035295	0.4236538540	25.467	1.083	0.343	12.877	0.752
H12	315.798	1.190	0.3344533	0.7387671092	-154.513	0.495	0.611	8.707	0.816
H13	340.238	1.186	0.3281713	0.7434968234	-264.998	0.134	0.874	4.536	0.942
H2	356.171	-0.797	-3.1642416	0.0020830059	1828.976	6.974	0.001	32.674	0.124
H3	345.728	-0.641	-2.8896824	0.0047675367	1521.522	5.970	0.004	30.230	0.096
H4	346.107	0.480	-0.9147227	0.3626290955	1315.472	5.297	0.007	28.475	0.063
H5	340.919	1.300	0.5286838	0.5982449757	62.734	1.205	0.304	13.581	0.685
H6	363.105	1.993	1.7491926	0.0834537132	-226.797	0.259	0.772	6.299	0.960
H7	344.992	0.028	-1.7107209	0.0903623671	2296.572	8.502	0.000	36.074	0.000
H8	321.534	0.930	-0.1226089	0.9026731286	4347.332	15.200	0.000	48.236	0.081
H9	310.567	2.980	3.4866633	0.0007393608	3418.972	12.168	0.000	43.157	0.531

# Gráfico
p1 <- plot(reg_model)
p2 <- plot(reg_model,
           x.lab = "Índice ambiental",
           y.lab = "Massa de Mil Grãos (g)",
           plot_theme = theme_metan_minimal())
p3 <- plot(reg_model, type = 2)

# reunir os plots
arrange_ggplot((p1 + p2), p3, ncol = 1,
               guides = "collect",
               tag_levels = "A",
               tag_suffix = ")")

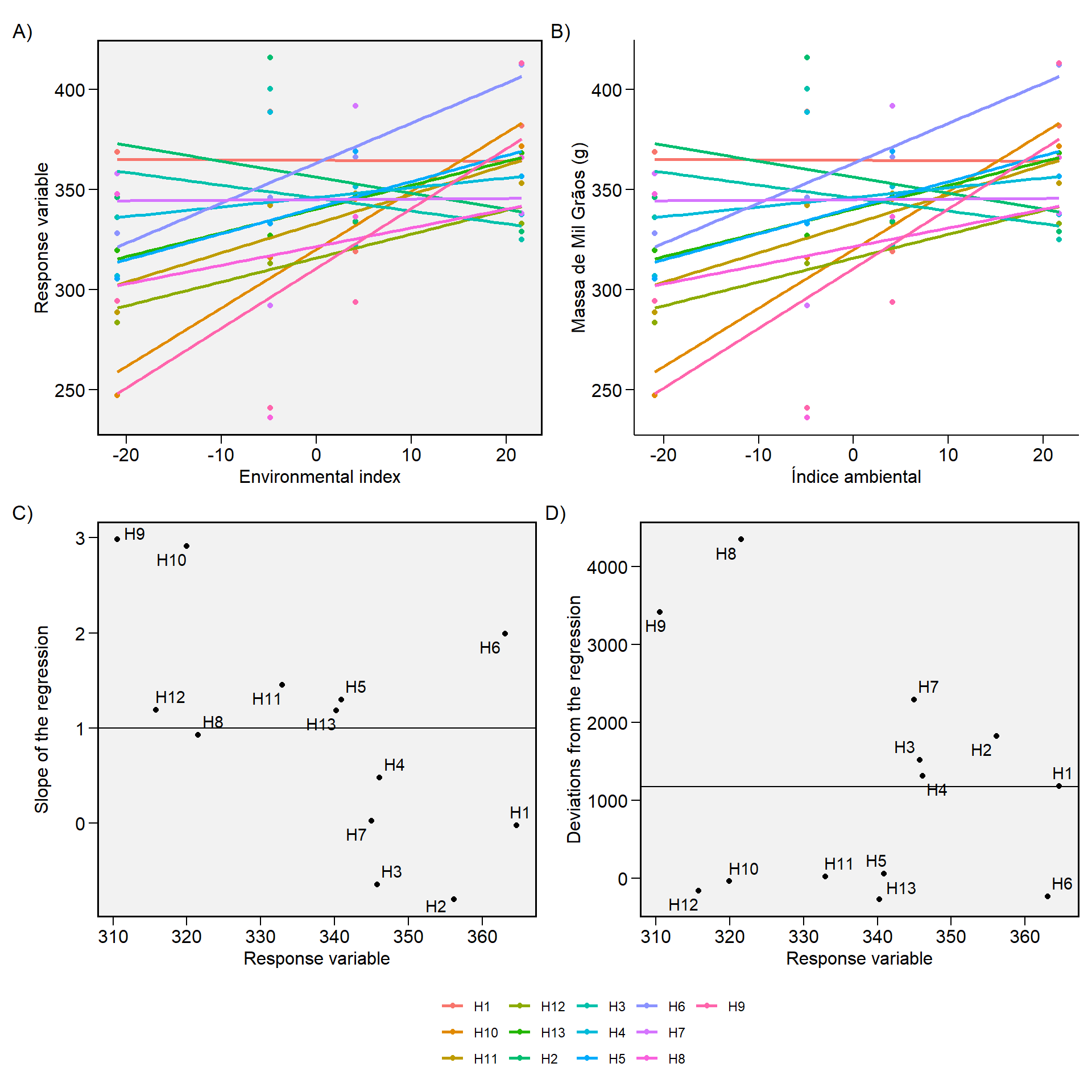
Índice de confiança genotípica

Annicchiarico (1992)⁴ propôs um método de estabilidade em que o parâmetro de estabilidade é medido pela superioridade do genótipo em relação à média de cada ambiente, de acordo com o seguinte modelo:

$$ {Z_ {ij}} = \frac {{{Y_ {ij}}}} {{{{\bar Y} _ {. J}}}} \times 100 $$ O índice de confiança genotípica do genótipo \(i\) (\(W_i\)) é então estimado da seguinte forma:

$$ W_i = Z_ {i.} / E - \alpha \times sd(Z_{i.}) $$ Onde \(\alpha\) é o quantil da distribuição normal padrão em uma dada probabilidade de erro (\(\alpha \approx 1,64 \alpha 0,05\)). O método é implementado usando a função Annicchiarico(). O índice de confiança é estimado considerando todos os ambientes, ambientes favoráveis (índice positivo) e ambientes desfavoráveis (índice negativo).

ann1 <- Annicchiarico(df_ge,
                      env = ENV,
                      gen = GEN,
                      rep = BLOCO,
                      resp = everything(),
                      verbose = FALSE)

# Wi
gmd(ann1) %>% print_tbl()
## Class of the model: Annicchiarico
## Variable extracted: Wi

GEN	ALT_PLANT	ALT_ESP	COMPES	DIAMES	COMP_SAB	DIAM_SAB	MGE	NFIL	MMG	NGE
H1	99.317	100.724	98.724	101.093	98.724	96.970	103.686	99.249	100.459	91.829
H10	88.284	84.746	97.320	94.301	91.868	97.185	88.240	92.785	86.375	95.169
H11	91.871	86.621	97.448	95.913	94.219	98.024	95.253	90.163	94.645	95.045
H12	90.999	81.972	91.209	96.745	93.802	90.189	84.650	98.175	90.942	90.930
H13	94.449	91.370	95.457	99.175	95.254	95.548	93.585	102.707	99.215	94.549
H2	98.144	89.381	98.173	98.973	93.203	96.692	98.078	95.687	95.690	97.699
H3	96.619	91.333	90.269	98.041	94.393	94.104	89.909	92.443	93.396	89.245
H4	97.694	95.229	100.839	97.376	95.165	100.665	100.550	91.344	95.472	101.952
H5	99.462	95.434	100.237	98.267	96.982	102.230	102.157	93.330	97.287	100.812
H6	97.707	99.749	97.930	102.562	99.271	98.663	96.757	97.304	103.558	89.813
H7	92.264	91.922	96.634	98.231	98.731	96.497	90.193	97.969	93.005	95.396
H8	87.109	78.137	93.663	95.019	92.440	94.651	80.447	95.255	83.628	90.798
H9	90.185	87.555	94.189	92.809	94.146	95.306	76.645	91.159	79.349	88.262

# Ranques
gmd(ann1, "rank")  %>% print_tbl()
## Class of the model: Annicchiarico
## Variable extracted: rank

GEN	ALT_PLANT	ALT_ESP	COMPES	DIAMES	COMP_SAB	DIAM_SAB	MGE	NFIL	MMG	NGE
H1	2	1	3	2	3	6	1	2	2	8
H10	12	11	7	12	13	5	10	9	11	5
H11	9	10	6	10	8	4	6	13	7	6
H12	10	12	12	9	10	13	11	3	10	9
H13	7	6	9	3	5	9	7	1	3	7
H2	3	8	4	4	11	7	4	6	5	3
H3	6	7	13	7	7	12	9	10	8	12
H4	5	4	1	8	6	2	3	11	6	1
H5	1	3	2	5	4	1	2	8	4	2
H6	4	2	5	1	1	3	5	5	1	11
H7	8	5	8	6	2	8	8	4	9	4
H8	13	13	11	11	12	11	12	7	12	10
H9	11	9	10	13	9	10	13	12	13	13

# classificação dos ambientes
ann1$ALT_PLANT$environments  %>% print_tbl()

ENV	Y	index	class
A1	2.793	0.308	favorable
A2	2.462	-0.023	unfavorable
A3	2.167	-0.318	unfavorable
A4	2.518	0.033	favorable

Índice de superioridade

A função superiority() implementa o método não paramétrico proposto por Lin e Binns (1988)⁵, que considera que uma medida de superioridade geral de cultivar para dados de ensaios multiambientes é definida como a soma do quadrado da distância média entre a resposta da cultivar e a resposta máxima calculada em todos os locais, de acordo com o seguinte modelo.

$$ P_i = \sum \limits_ {j = 1} ^ n {(y_ {ij} - y _ {. J}) ^ 2 / (2n)} $$ onde *n* é o número de ambientes

Semelhante ao índice de confiança genotípica, o índice de superioridade é calculado por todos os ambientes, favoráveis e desfavoráveis.

super <- superiority(df_ge,
                     env = ENV,
                     gen = GEN,
                     resp = everything(),
                     verbose = FALSE)
gmd(super) %>% print_tbl()
## Class of the model: superiority
## Variable extracted: Pi_a

GEN	ALT_PLANT	ALT_ESP	COMPES	DIAMES	COMP_SAB	DIAM_SAB	MGE	NFIL	MMG	NGE
H1	0.026	0.007	1.287	1.418	3.055	1.533	332.263	1.987	873.628	6441.658
H10	0.151	0.094	1.226	11.544	10.934	1.271	1147.318	3.693	3576.987	5152.155
H11	0.116	0.085	1.296	9.327	9.207	1.153	918.019	4.384	2171.711	5686.694
H12	0.103	0.106	3.130	8.863	9.456	3.591	1566.449	1.916	3447.948	6837.431
H13	0.069	0.062	1.632	3.080	5.278	1.557	684.533	0.411	1798.489	4401.477
H2	0.029	0.026	1.029	2.492	6.540	1.355	337.227	2.156	1365.866	4122.825
H3	0.043	0.021	3.035	4.607	6.801	2.131	823.879	3.320	1745.780	8201.163
H4	0.040	0.021	0.640	6.287	6.982	0.653	361.730	4.540	1487.961	3193.574
H5	0.040	0.034	0.562	5.497	5.948	0.441	386.551	3.213	1824.117	2095.889
H6	0.033	0.014	0.716	0.621	4.412	0.695	404.197	1.967	895.035	6042.938
H7	0.109	0.064	1.178	6.168	4.808	1.050	1104.620	2.053	2627.212	6135.408
H8	0.161	0.126	1.971	11.403	10.182	1.696	1788.539	3.018	4741.914	7287.795
H9	0.124	0.068	2.031	15.070	8.573	1.667	2072.695	4.653	5702.604	7956.043

Estratificação ambiental

Um método que combina análise de estabilidade e estratificação ambiental usando análise fatorial foi proposto por Murakami e Cruz (2004)⁶. Este método é implementado com a função ge_factanal(), da seguinte forma:

fato <- ge_factanal(df_ge, 
                    env = ENV,
                    gen = GEN,
                    rep = BLOCO,
                    resp = everything(),
                    verbose = FALSE,
                    mineval = 0.7)

# plot
plot(fato, var = "MMG")

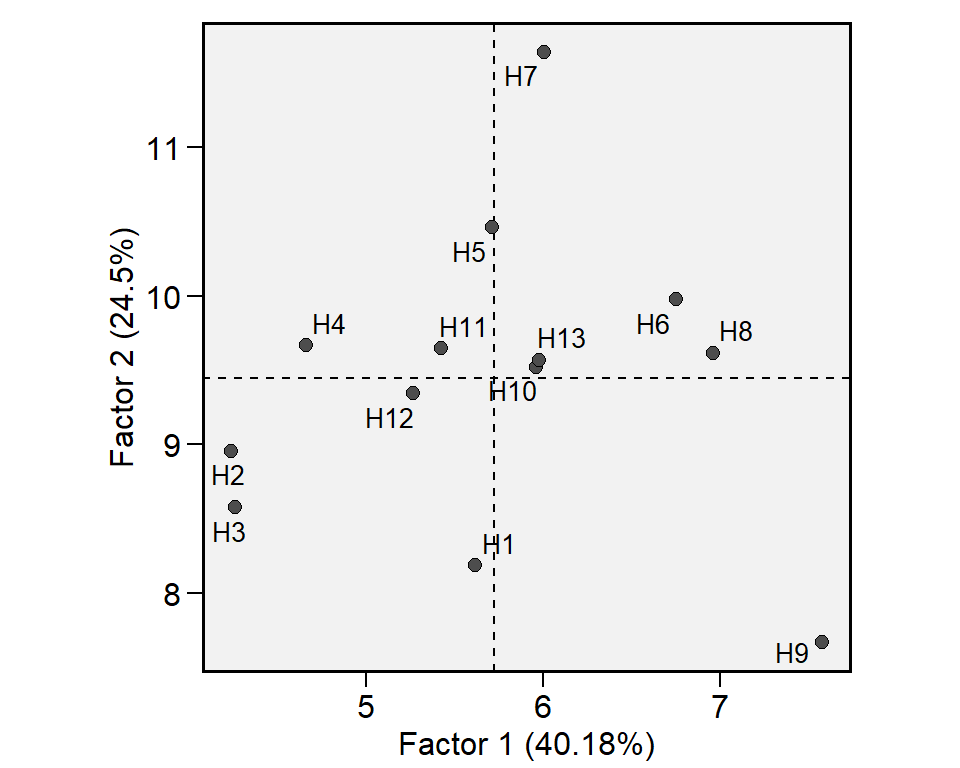
# Autovalores e variância
print_tbl(fato$MMG$PCA)

PCA	Eigenvalues	Variance	Cumul_var
PC1	1.607	40.178	40.178
PC2	0.980	24.500	64.678
PC3	0.912	22.807	87.485
PC4	0.501	12.515	100.000

# Cargas fatoriais após rotação varimax
print_tbl(fato$MMG$FA)

Env	FA1	FA2	FA3	Communality	Uniquenesses
A1	0.831	-0.288	-0.065	0.778	0.222
A2	-0.849	-0.135	-0.223	0.788	0.212
A3	-0.093	0.059	-0.983	0.978	0.022
A4	-0.069	0.973	-0.060	0.955	0.045

# Estratificação
print_tbl(fato$MMG$env_strat)

Env	Factor	Mean	Min	Max	CV
A1	FA1	360.337	325.013	413.088	8.096
A2	FA1	333.815	236.281	415.675	16.856
A4	FA2	342.796	293.694	391.762	7.228
A3	FA3	317.718	247.261	368.768	10.814

A função ge_stats()

A maneira mais fácil de calcular os índices de estabilidade mencionados acima é usando a função ge_stats(). É uma função “wrapper” que computa todos os índices de estabilidade de uma única vez. Para obter os resultados em um arquivo “pronto para ler”, use gmd().

stat_ge <- ge_stats(df_ge,
                    env = ENV,
                    gen = GEN,
                    rep = BLOCO,
                    resp = c(MMG, MGE))
## Evaluating trait MMG |======================                     | 50% 00:00:03 
Evaluating trait MGE |===========================================| 100% 00:00:05 
# estatisticas
gmd(stat_ge, "stats") %>% print_tbl()
## Class of the model: ge_stats
## Variable extracted: stats

var	GEN	Y	CV	ACV	POLAR	Var	Shukla	Wi_g	Wi_f	Wi_u	Ecoval	bij	Sij	R2	ASV	SIPC	EV	ZA	WAAS	WAASB	HMGV	RPGV	HMRPGV	Pi_a	Pi_f	Pi_u	Gai	S1	S2	S3	S6	N1	N2	N3	N4
MGE	H1	183.747	10.498	12.083	-0.247	1116.387	11.555	99.657	98.888	103.555	414.699	0.844	-77.149	0.907	2.707	1.573	0.008	0.071	0.782	1.155	179.691	1.051	1.050	332.263	275.953	388.573	182.951	0.167	3.583	0.081	0.162	1.25	0.250	0.345	0.035
MGE	H10	163.893	19.491	17.377	0.069	3061.262	160.408	79.699	92.027	73.624	1548.269	1.395	18.268	0.904	2.809	2.830	0.050	0.091	0.895	1.160	161.696	0.955	0.951	1147.318	493.895	1800.741	161.345	1.333	11.667	5.556	1.778	2.50	0.263	0.311	0.140
MGE	H11	167.240	12.166	11.347	-0.301	1241.912	-20.805	93.105	90.933	94.996	168.262	0.917	-105.803	0.963	0.994	0.981	0.006	0.032	0.321	0.421	166.502	0.974	0.974	918.019	655.031	1181.006	166.278	0.333	0.917	1.667	0.952	0.75	0.088	0.095	0.038
MGE	H12	157.474	13.961	11.385	-0.298	1450.104	287.701	75.021	86.923	62.608	2517.655	0.715	232.821	0.501	8.213	3.614	0.040	0.187	2.150	2.122	158.882	0.932	0.928	1566.449	939.068	2193.831	156.298	0.500	11.333	6.294	2.118	2.50	0.250	0.299	0.051
MGE	H13	179.838	16.076	17.635	0.082	2507.555	790.862	77.725	68.274	84.912	6349.416	0.637	835.854	0.230	6.391	6.619	0.296	0.202	1.952	1.736	176.064	1.036	1.025	684.533	749.402	619.664	178.152	2.000	30.333	9.059	1.882	4.50	1.000	0.867	0.364
MGE	H2	186.999	15.420	18.457	0.121	2494.460	783.810	82.899	87.203	95.440	6295.715	0.639	827.773	0.233	14.353	4.516	0.088	0.282	3.366	2.858	181.481	1.067	1.059	337.227	561.094	113.359	185.339	0.833	24.917	6.135	1.351	3.75	1.071	0.910	0.175
MGE	H3	169.456	17.398	16.711	0.035	2607.508	457.681	78.288	74.688	82.277	3812.115	0.970	505.775	0.513	11.355	4.243	0.061	0.240	2.813	1.892	167.189	0.984	0.979	823.879	998.956	648.801	167.511	0.000	12.667	8.182	2.182	3.00	0.353	0.363	0.000
MGE	H4	184.260	14.858	17.208	0.061	2248.709	210.678	92.036	95.538	84.770	1931.096	1.064	189.975	0.716	5.337	4.136	0.075	0.160	1.694	1.633	178.833	1.051	1.048	361.730	245.252	478.208	182.562	0.667	10.000	1.378	0.757	2.50	0.556	0.577	0.140
MGE	H5	183.635	8.399	9.653	-0.442	713.629	119.666	95.631	87.860	109.197	1238.005	0.606	-33.097	0.731	1.727	1.796	0.022	0.054	0.519	1.184	180.090	1.052	1.050	386.551	402.287	370.815	183.123	0.167	13.667	3.757	1.189	2.00	0.500	0.674	0.035
MGE	H6	187.999	23.075	27.950	0.482	5645.769	938.289	80.515	80.748	70.620	7472.134	1.609	852.492	0.652	13.863	4.217	0.082	0.268	3.218	3.098	179.051	1.063	1.053	404.197	308.903	499.492	184.086	0.333	34.000	10.250	2.250	5.00	0.833	0.842	0.056
MGE	H7	171.051	15.553	15.256	-0.044	2123.393	616.384	77.098	75.298	71.682	5020.702	0.658	624.746	0.290	11.555	5.093	0.079	0.263	3.027	2.351	169.147	0.994	0.987	1104.620	632.640	1576.600	169.516	0.333	30.917	10.571	2.286	4.75	0.633	0.688	0.048
MGE	H8	159.860	24.757	20.877	0.228	4698.738	971.105	63.670	92.782	47.656	7722.038	1.247	1114.690	0.471	16.164	5.511	0.115	0.328	3.887	2.995	157.575	0.938	0.924	1788.539	370.246	3206.831	155.981	0.333	24.250	5.333	1.333	2.75	0.344	0.533	0.042
MGE	H9	152.753	28.202	21.486	0.253	5567.447	807.372	61.157	93.700	55.597	6475.147	1.699	603.283	0.737	12.230	4.923	0.077	0.267	3.106	3.324	151.076	0.902	0.890	2072.695	434.254	3711.136	148.265	1.000	26.250	12.400	2.800	4.25	0.425	0.493	0.111
MMG	H1	364.627	8.653	11.222	0.026	2986.494	1428.010	89.756	84.496	115.774	11929.793	-0.022	1186.877	0.000	7.758	9.280	0.115	0.233	2.723	3.488	357.771	1.062	1.057	873.628	1568.453	178.803	363.550	1.667	20.250	7.865	1.568	3.25	1.083	0.820	0.351
MMG	H10	319.960	16.732	13.805	0.206	8598.665	1443.749	75.316	99.000	66.671	12049.653	2.914	-36.357	0.937	6.579	8.775	0.119	0.196	2.154	2.473	318.632	0.953	0.946	3576.987	976.033	6177.942	316.356	1.667	24.917	7.435	1.913	3.75	0.469	0.524	0.202
MMG	H11	332.915	8.971	8.492	-0.216	2676.187	200.613	89.534	95.619	83.154	2582.691	1.456	25.467	0.752	3.549	4.588	0.024	0.110	1.260	0.801	332.381	0.986	0.984	2171.711	1379.858	2963.563	331.848	1.167	11.333	3.231	1.231	2.00	0.286	0.389	0.156
MMG	H12	315.798	7.420	5.850	-0.540	1647.118	-5.568	87.709	89.102	86.260	1012.547	1.190	-154.513	0.816	0.981	2.640	0.012	0.053	0.558	1.589	319.446	0.946	0.946	3447.948	2456.959	4438.937	315.125	0.667	3.667	0.846	0.923	1.50	0.143	0.154	0.062
MMG	H13	340.238	6.390	6.522	-0.445	1418.101	-93.119	97.470	100.300	96.135	345.814	1.186	-264.998	0.942	2.451	0.870	0.001	0.038	0.514	0.423	338.968	1.003	1.003	1798.489	1021.110	2575.868	339.724	0.000	2.667	0.667	0.533	1.00	0.154	0.218	0.000
MMG	H2	356.171	11.316	13.531	0.188	4873.365	2751.227	81.518	87.132	98.505	22006.597	-0.797	1828.976	0.124	19.026	9.104	0.081	0.338	4.407	3.857	350.636	1.044	1.035	1365.866	2601.310	130.422	354.565	1.000	30.333	9.733	2.133	4.50	0.692	0.734	0.154
MMG	H3	345.728	10.622	11.458	0.044	4045.579	2308.528	80.412	87.758	96.442	18635.273	-0.641	1521.522	0.096	17.311	8.814	0.073	0.316	4.097	3.080	342.651	1.019	1.011	1745.780	3162.932	328.628	344.351	1.333	27.667	12.600	2.720	4.50	0.562	0.588	0.172
MMG	H4	346.107	9.816	10.628	-0.021	3462.326	1240.023	85.656	87.827	83.354	10498.197	0.480	1315.472	0.063	12.974	6.624	0.041	0.237	3.070	2.769	342.804	1.018	1.014	1487.961	1831.223	1144.699	344.861	0.500	14.250	3.600	1.333	2.75	0.458	0.503	0.077
MMG	H5	340.919	8.196	8.423	-0.223	2342.327	185.815	92.522	93.187	93.797	2470.003	1.300	62.734	0.685	0.984	3.799	0.030	0.072	0.738	0.476	338.999	1.005	1.004	1824.117	932.079	2716.156	340.044	1.333	12.917	3.452	1.097	2.25	0.321	0.498	0.213
MMG	H6	363.105	9.968	12.742	0.136	3930.178	292.999	98.565	101.865	102.976	3286.247	1.993	-226.797	0.960	5.731	4.614	0.022	0.134	1.636	0.591	355.852	1.055	1.054	895.035	162.728	1627.343	361.789	0.000	10.250	1.000	0.600	1.75	0.438	0.693	0.000
MMG	H7	344.992	12.075	12.930	0.149	5206.204	2265.054	79.957	80.262	70.786	18304.208	0.028	2296.572	0.000	9.611	12.375	0.172	0.300	3.442	2.550	341.194	1.016	1.008	2627.212	1406.081	3848.343	343.060	0.167	27.333	9.061	2.061	4.50	0.818	0.787	0.029
MMG	H8	321.534	18.071	15.165	0.288	10128.429	3529.663	67.320	95.892	45.138	27934.690	0.930	4347.332	0.081	19.829	11.185	0.134	0.384	4.909	4.496	319.330	0.960	0.945	4741.914	1327.984	8155.844	317.081	0.833	26.000	8.154	1.846	3.50	0.500	0.589	0.111
MMG	H9	310.567	23.426	17.434	0.409	15879.870	4262.573	62.157	66.471	58.698	33516.082	2.980	3418.972	0.531	21.320	13.615	0.175	0.436	5.499	5.127	308.772	0.931	0.916	5702.604	2404.298	9000.910	304.625	0.667	23.583	18.000	3.200	3.75	0.341	0.467	0.074

# Ranques
gmd(stat_ge, "ranks") %>% print_tbl()
## Class of the model: ge_stats
## Variable extracted: ranks

var	GEN	Y_R	CV_R	ACV_R	POLAR_R	Var_R	Shukla_R	Wi_g_R	Wi_f_R	Wi_u_R	Ecoval_R	Sij_R	R2_R	ASV_R	SIPC_R	EV_R	ZA_R	WAAS_R	WAASB_R	HMGV_R	RPGV_R	HMRPGV_R	Pi_a_R	Pi_f_R	Pi_u_R	Gai_R	S1_R	S2_R	S3_R	S6_R	N1_R	N2_R	N3_R	N4_R
MGE	H1	4	2	4	4	2	2	1	1	2	2	3	2	3	2	2	3	3	2	3	5	4	1	2	3	4	2.5	2	1	1	2.0	2.5	4	2.5
MGE	H10	10	10	8	8	10	4	7	5	8	4	1	3	4	4	5	4	4	3	10	10	10	10	7	10	10	12.0	5	6	7	5.0	4.0	3	10.5
MGE	H11	9	3	2	2	3	1	3	6	4	1	4	1	1	1	1	1	1	1	9	9	9	8	10	8	9	5.5	1	3	3	1.0	1.0	1	4.0
MGE	H12	12	4	3	3	4	6	11	9	11	6	6	9	7	5	4	6	7	8	11	12	11	11	12	11	11	8.0	4	8	9	5.0	2.5	2	7.0
MGE	H13	6	8	9	9	8	10	9	13	5	10	11	13	6	13	13	7	6	6	6	6	6	6	11	6	6	13.0	11	10	8	11.0	12.0	12	13.0
MGE	H2	2	6	10	10	7	9	5	8	3	9	10	12	12	9	11	12	12	10	1	1	1	2	8	1	1	10.0	9	7	6	9.0	13.0	13	12.0
MGE	H3	8	9	6	6	9	7	8	12	7	7	7	8	8	8	6	8	8	7	8	8	8	7	13	7	8	1.0	6	9	10	8.0	6.0	5	1.0
MGE	H4	3	5	7	7	6	5	4	2	6	5	5	6	5	6	7	5	5	5	5	4	5	3	1	4	5	9.0	3	2	2	5.0	9.0	8	10.5
MGE	H5	5	1	1	1	1	3	2	7	1	3	2	5	2	3	3	2	2	4	2	3	3	4	5	2	3	2.5	7	4	4	3.0	8.0	9	2.5
MGE	H6	1	11	13	13	13	12	6	10	10	12	12	7	11	7	10	11	11	12	4	2	2	5	3	5	2	5.5	13	11	11	13.0	11.0	11	8.0
MGE	H7	7	7	5	5	5	8	10	11	9	8	9	11	9	11	9	9	9	9	7	7	7	9	9	9	7	5.5	12	12	12	12.0	10.0	10	6.0
MGE	H8	11	12	11	11	11	13	12	4	13	13	13	10	13	12	12	13	13	11	12	11	12	12	4	12	12	5.5	8	5	5	7.0	5.0	7	5.0
MGE	H9	13	13	12	12	12	11	13	3	12	11	8	4	10	10	8	10	10	13	13	13	13	13	6	13	13	11.0	10	13	13	10.0	7.0	6	9.0
MMG	H1	1	4	6	6	5	7	4	11	1	7	7	12	7	10	9	7	7	10	1	1	1	1	8	2	1	12.5	7	8	7	7.0	13.0	13	13.0
MMG	H10	11	11	11	11	11	8	11	3	11	8	2	3	6	7	10	6	6	6	12	11	10	11	3	11	11	12.5	9	7	9	9.5	8.0	7	11.0
MMG	H11	9	5	4	4	4	4	5	5	9	4	1	5	4	4	4	4	4	4	9	9	9	8	6	8	9	9.0	4	4	5	4.0	3.0	3	9.0
MMG	H12	12	2	1	1	2	2	6	7	7	2	4	4	1	2	2	2	2	5	10	12	11	10	11	10	12	5.5	2	2	3	2.0	1.0	1	4.0
MMG	H13	8	1	2	2	1	1	2	2	5	1	6	2	3	1	1	1	1	1	8	8	8	6	4	6	8	1.5	1	1	1	1.0	2.0	2	1.5
MMG	H2	3	9	10	10	9	11	8	10	3	11	10	8	11	9	8	11	11	11	3	3	3	3	12	1	3	8.0	13	11	11	12.0	11.0	11	8.0
MMG	H3	5	8	7	7	8	10	9	9	4	10	9	9	10	8	7	10	10	9	5	4	5	5	13	3	5	10.5	12	12	12	12.0	10.0	8	10.0
MMG	H4	4	6	5	5	6	6	7	8	8	6	8	11	9	6	6	8	8	8	4	5	4	4	9	4	4	4.0	6	6	6	6.0	7.0	6	6.0
MMG	H5	7	3	3	3	3	3	3	6	6	3	3	6	2	3	5	3	3	2	7	7	7	7	2	7	7	10.5	5	5	4	5.0	4.0	5	12.0
MMG	H6	2	7	8	8	7	5	1	1	2	5	5	1	5	5	3	5	5	3	2	2	2	2	1	5	2	1.5	3	3	2	3.0	6.0	10	1.5
MMG	H7	6	10	9	9	10	9	10	12	10	9	11	13	8	12	12	9	9	7	6	6	6	9	7	9	6	3.0	11	10	10	12.0	12.0	12	3.0
MMG	H8	10	12	12	12	12	12	12	4	13	12	13	10	12	11	11	12	12	12	11	10	12	12	5	12	10	7.0	10	9	8	8.0	9.0	9	7.0
MMG	H9	13	13	13	13	13	13	13	13	12	13	12	7	13	13	13	13	13	13	13	13	13	13	10	13	13	5.5	8	13	13	9.5	5.0	4	5.0

Também é possível obter a correlação de postos de Spearman entre os índices de estabilidade usando corr_stab_ind().

corr_stab_ind(stat_ge)

---

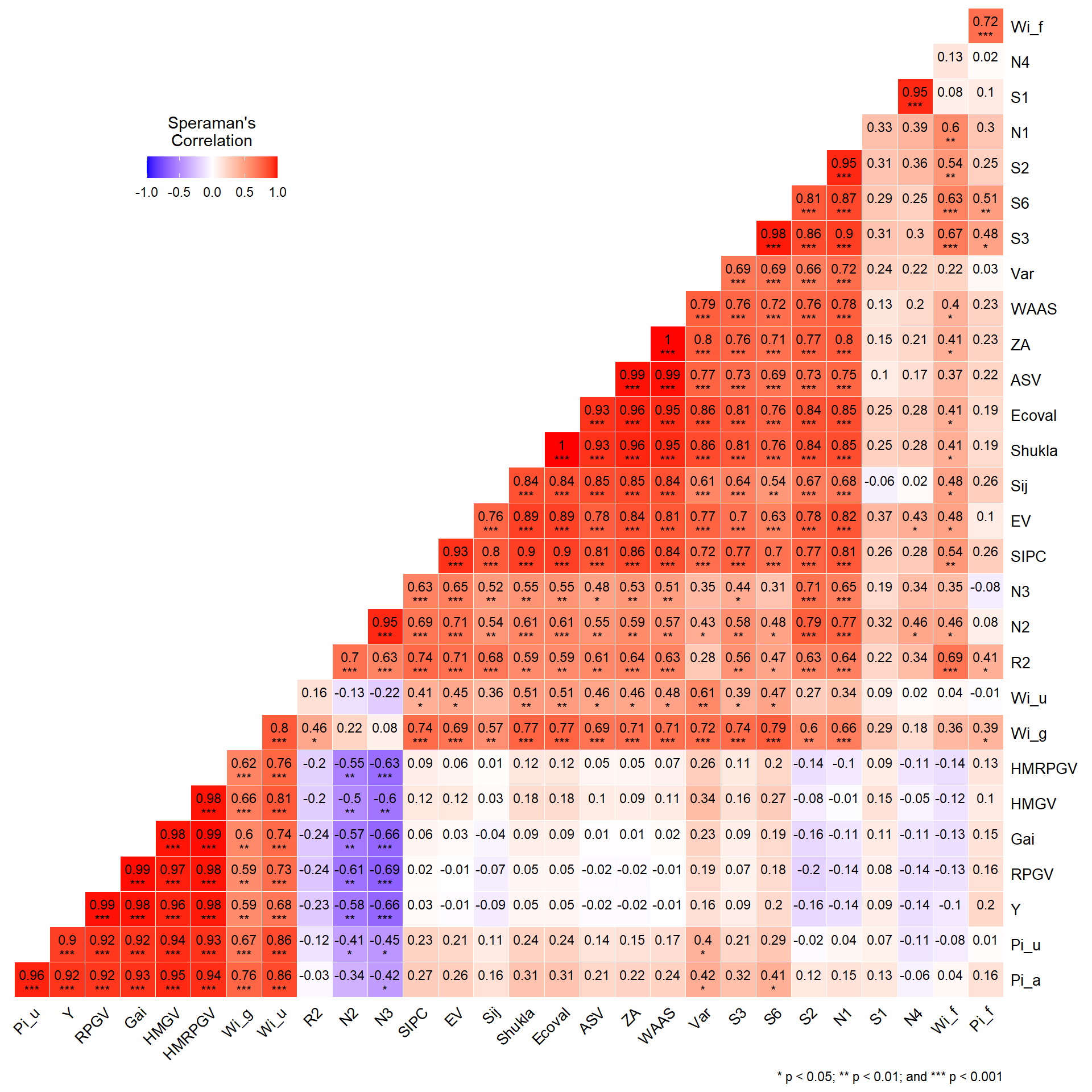
1. Robertson, A. (1959). Experimental design on the measurement of heritabilities and genetic correlations: Biometrical genetics. In Biometrical genetics. Pergamon. ↩︎

2. CRUZ, C.D.; CASTOLDI, F.L. Decomposição da interação genótipos x ambientes em partes simples e complexa. Revista Ceres, v.38, n.219, p.422-430, 1991. ↩︎

3. Eberhart, S. A., & Russell, W. A. (1966). Stability parameters for comparing varieties. Crop Science, 6(1), 36–40. https://doi.org/10.2135/cropsci1966.0011183X000600010011x ↩︎

4. Annicchiarico, P. (1992). Cultivar adaptation and recommendation from alfalfa trials in Northern Italy. Journal of Genetics and Breeding, 46, 269–278. ↩︎

5. Lin, C.S.; & Binns, M.R. (1988). A superiority measure of cultivar performance for cultivar x location data. Canadian Journal of Plant Science, 68, 193-198. https://cdnsciencepub.com/doi/abs/10.4141/cjps88-018 ↩︎

6. Murakami, D. M., & Cruz, C. D. (2004). Proposal of methodologies for environment stratification and analysis of genotype adaptability. Cropp Breeding and Applied Biotechnology, 4(1), 7–11. https://doi.org/10.12702/1984-7033.v04n01a02 ↩︎