library(metan)
## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2
## |=========================================================|
## | Multi-Environment Trial Analysis (metan) v1.15.0        |
## | Author: Tiago Olivoto                                   |
## | Type 'citation('metan')' to know how to cite metan      |
## | Type 'vignette('metan_start')' for a short tutorial     |
## | Visit 'https://bit.ly/pkgmetan' for a complete tutorial |
## |=========================================================|
library(rio)

# gerar tabelas html
print_tbl <- function(table, digits = 3, ...){
  knitr::kable(table, booktabs = TRUE, digits = digits, ...)
}


df_ge <- import("http://bit.ly/df_ge", setclass = "tbl")
inspect(df_ge, verbose = FALSE) %>% print_tbl()

O modelo AMMI

A análise AMMI utiliza análise aditiva de variância aos fatores principais (genótipo e ambiente) e decomposição por valores singulares ao residual do modelo aditivo, isto é, o efeito da GEI somado ao erro experimental. Esta matriz dos efeitos não aditivos, então, pode ser aproximadamente exibida por meio de biplots¹. Este método tem ganhado destaque nas últimas décadas, principalmente devido a rápida evolução computacional, o que tornou possível as complexas decomposições de matrizes de alta ordem.

De posse de uma matriz de dupla entrada oriunda de ensaios multiambientes, a estimativa da variável resposta do \(i\)-ésimo genótipo no \(i\)-ésimo ambiente é obtida utilizando AMMI de acordo com o seguinte modelo:

$$ {y_{ij}} = \mu + {\alpha_i} + {\tau_j} + \sum\limits_{k = 1}^k {{\lambda _k}{a_{ik}}} {t_{jk}} + {\rho _{ij}} + {\varepsilon _{ij}} $$

onde \({\lambda_k}\) é o valor singular para o \(k\)-ésimo eixo do componente principal; \(a_{ik}\) é o \(i\)-ésimo elemento do \(k\)-ésimo autovetor de genótipos; \(t_{jk}\) é o \(j\)-ésimo elemento do \(k\)-ésimo autovetor de ambientes. Um resíduo \(\rho _{ij}\) permanece, se todos os \(k\)-PCAs não são considerados, onde \(k\) = \(min(G-1; E-1)\). O modelo AMMI é computado com a função performs_ammi()

ammi_model <- 
  performs_ammi(df_ge,
                env = ENV,
                gen = GEN,
                rep = BLOCO,
                resp = MGE:MMG,
                verbose = FALSE)

Analise residual

\(\hat y_{ij} = \bar y_{i.} + \bar y_{.j} - \bar y_{..}\)

plot(ammi_model)

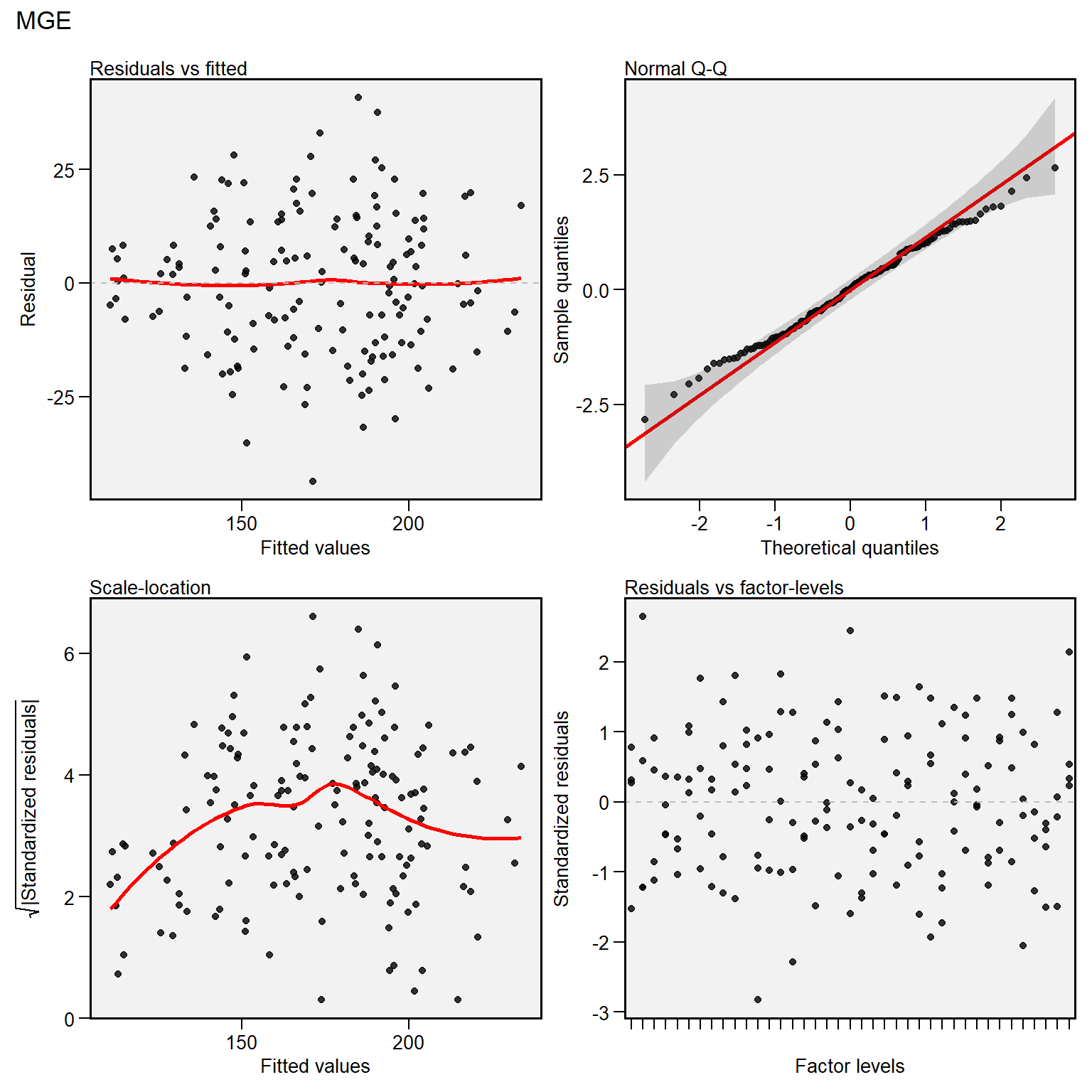
Escoha do número de IPCAs retidos

A análise AMMI aplica a técnica de decomposição por valores singulares na matriz dos efeitos não aditivos do modelo (A). Logo, esta matriz pode ser aproximada pela pelo seguinte modelo: \(\mathbf{A = U \lambda V^T}\), onde onde \(U\) é uma matriz \(g\) \(\times\) \(e\) contendo os vetores singulares de \(\mathbf{AA^T}\) e formam a base ortonormal para os efeitos de genótipos; \(\mathbf{V^T}\) é uma matriz \(e\) \(\times\) \(e\) que contém os vetores singulares de \(\mathbf{A^TA}\) e formam a base ortonormal para os efeitos de ambientes; e \(\mathbf{\lambda}\) é uma matriz diagonal \(e\) \(\times\) \(e\) contendo \(k\)-valores singulares de \(\mathbf{A^{T}A}\) , onde \(k\) = \(min(G-1; E-1)\). Assim, diferentes modelos (dependendo do número de IPCAs utilizados) podem ser utilziados para estimar o rendimento do genótipo \(i\) no ambiente \(j\). A tabela abaixo mostra os possíveis modelos. No modelo AMMI0 apenas os efeitos aditivos são considerados. No modelo AMMI1, o primeiro termo multiplicativo é considerado, e assim por diante, até o modelo AMMIF, onde \(min(G-1;E-1)\) termos são considerados.

A escolha do número de IPCAs a ser utilizado é baseada em basicamente dois critérios de sucesso de análise: Postdiscritive sucess e Predictive sucess. Por definição, predictive sucess significa literalmente a afirmação prévia do que acontecerá em algum momento futuro. Neste contexto, testes de validação cruzada (cross-validation) podem ser utilizados para avaliar o sucesso preditivo dos membros de modelos da familia AMMI. Por outro lado, postdiscritive sucess significa fazer uma afirmação ou dedução sobre algo que aconteceu no passado. Na escolha do número de IPCAs da análise AMMI, \index{AMMI}este sucesso pode ser calculado utilizando testes como o proposto por Gollob (1968)².

• Postdiscritive sucess Testes de hipóteses são realizados e probabilidades de erro são atribuídas para cada membro da família de modelos AMMI utilizando a distribuição de graus de liberdade proposto por Gollob (1968)². Assim, é possível identificar qual é o número ideal de IPCAs a ser considerado na estimativa.

gmd(ammi_model, "ipca_pval") %>% print_tbl()
## Class of the model: performs_ammi
## Variable extracted: Pr(>F)

gmd(ammi_model, "ipca_expl") %>% print_tbl()
## Class of the model: performs_ammi
## Variable extracted: Proportion

gmd(ammi_model, "ipca_accum") %>% print_tbl()
## Class of the model: performs_ammi
## Variable extracted: Accumulated

\index{predictive sucess}

Utilizando a função cv_ammif(), é possível realizar um teste de validação cruzada para a família de modelos AMMI (AMMI0-AMMIF) usando dados com repetições. Automaticamente, a primeira validação é realizada considerando a AMMIF (todos possíveis IPCAs são usados). Considerando esse modelo, o conjunto de dados original é dividido em dois conjuntos de dados: dados de modelagem e dados de validação.

O conjunto de dados “modelagem” possui todas as combinações (genótipo vs ambiente) com o número de repetições informado no argumento nrepval. O conjunto de dados “validação” tem uma repetição. A divisão do conjunto de dados em dados de modelagem e validação depende do design informado. Considerando um delineamento de blocos completos casualizados (DBC)\index{DBC}, blocos completos são aleatoriamente selecionados dentro de ambientes, como sugerido por Piepho (1994)³. O bloco restante serve dados de validação. Se design = "CRD" for informado, assim declarando que um delineamento intericamente casualizado (DIC) \index{DIC} foi usado, observações são aleatoriamente selecionadas para cada tratamento (combinação genótipo-vs-ambiente). Este é o mesmo procedimento sugerido por Gauch (1988)⁴. Os valores estimados para o membro da família AMMI em estudo são então comparados com os dados de “validação” e um erro de predição \(\hat{z}_{ij}\) é estimado para cada tratamento. A raiz quadrada do quadrado médio da diferença de predição (RMSPD) é calculado. Este procedimento é repetido n vezes, utilizando o argumento nboot = n. Ao final do procedimento, o algorítimo armazena as n estimativas do RMSPD para o modelo em questão, e um novo modelo é então testado seguindo os mesmos passos. Uma barra de progresso é mostrada por padrão. Assim, é possível verificar o status do processo. Se necessário, a barra de progresso pode ser desabilitada informando o argumento verbose = FALSE na função.

# Validação cruzada para os membros de modelos da família AMMI
cvalida <- 
  cv_ammif(df_ge,
          env = ENV,
          gen = GEN,
          rep = BLOCO,
          resp = MGE,
          nboot = 20,
          verbose = FALSE)
p1 <- plot(cvalida)
p2 <- plot(cvalida,
          width.boxplot = 0.5,
          col.boxplot = "white",
          plot_theme = theme_metan_minimal())
p1 + p2

Valores estimados pelo modelo AMMI

predicted <- predict(ammi_model, naxis = c(3, 2, 1))
print_tbl(predicted$MGE)

Biplot AMMI1

p1 <- plot_scores(ammi_model)
p2 <- plot_scores(ammi_model,
                  x.lab = "Massa de grãos por espiga",
                  col.segm.env = "black",
                  col.gen = "gray",
                  col.env = "black",
                  highlight = c("H8", "H6", "H2"),
                  plot_theme = theme_metan_minimal())
arrange_ggplot(p1, p2, tag_levels = "a")

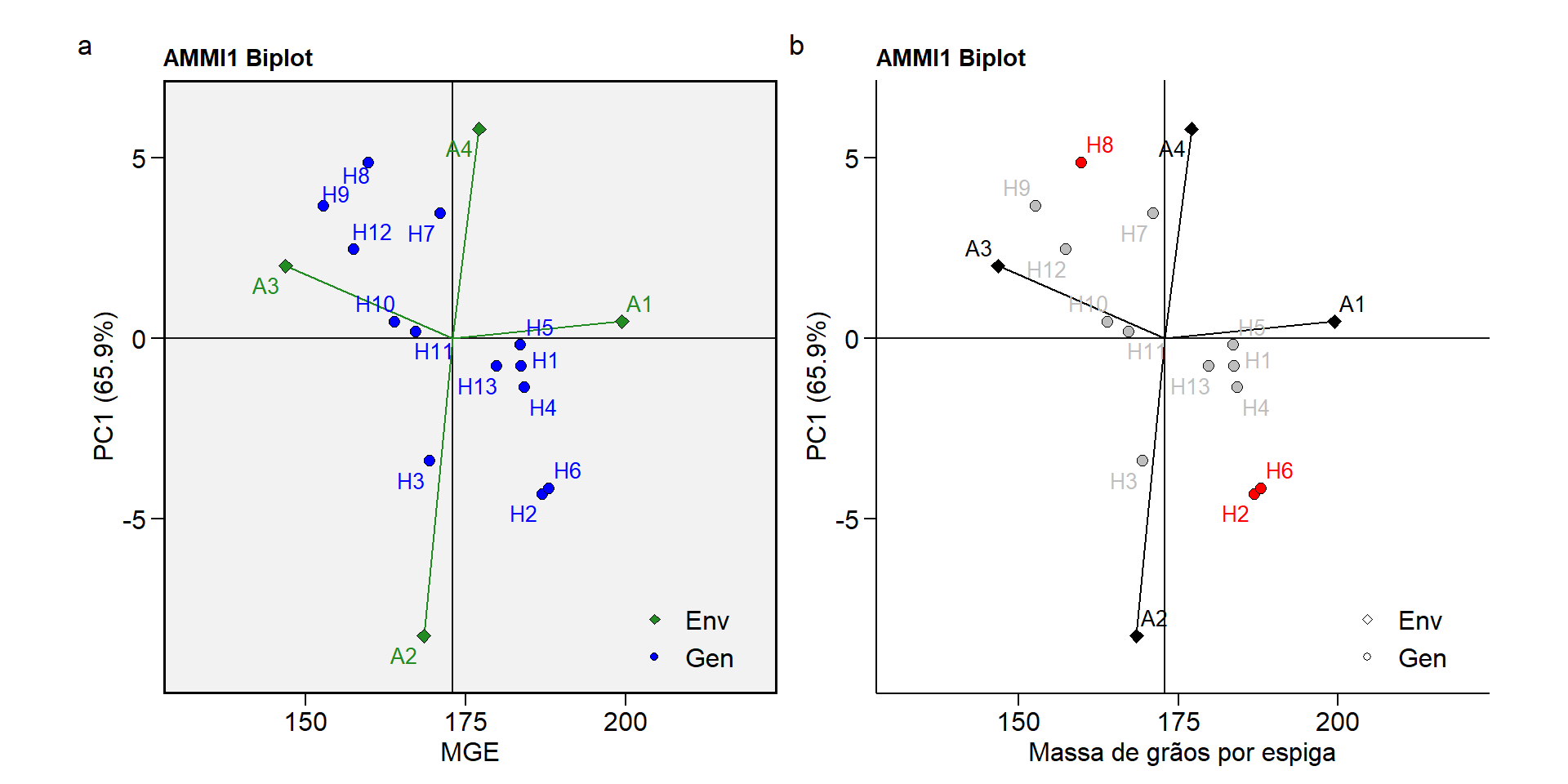
Biplot AMMI2

p3 <- plot_scores(ammi_model, type = 2)
p4 <- plot_scores(ammi_model,
                  type = 2,
                  col.segm.env = "black",
                  col.gen = "gray",
                  col.env = "black",
                  highlight = c("H8", "H6", "H2"),
                  plot_theme = theme_metan_minimal())

arrange_ggplot(p3, p4, tag_levels = "a")

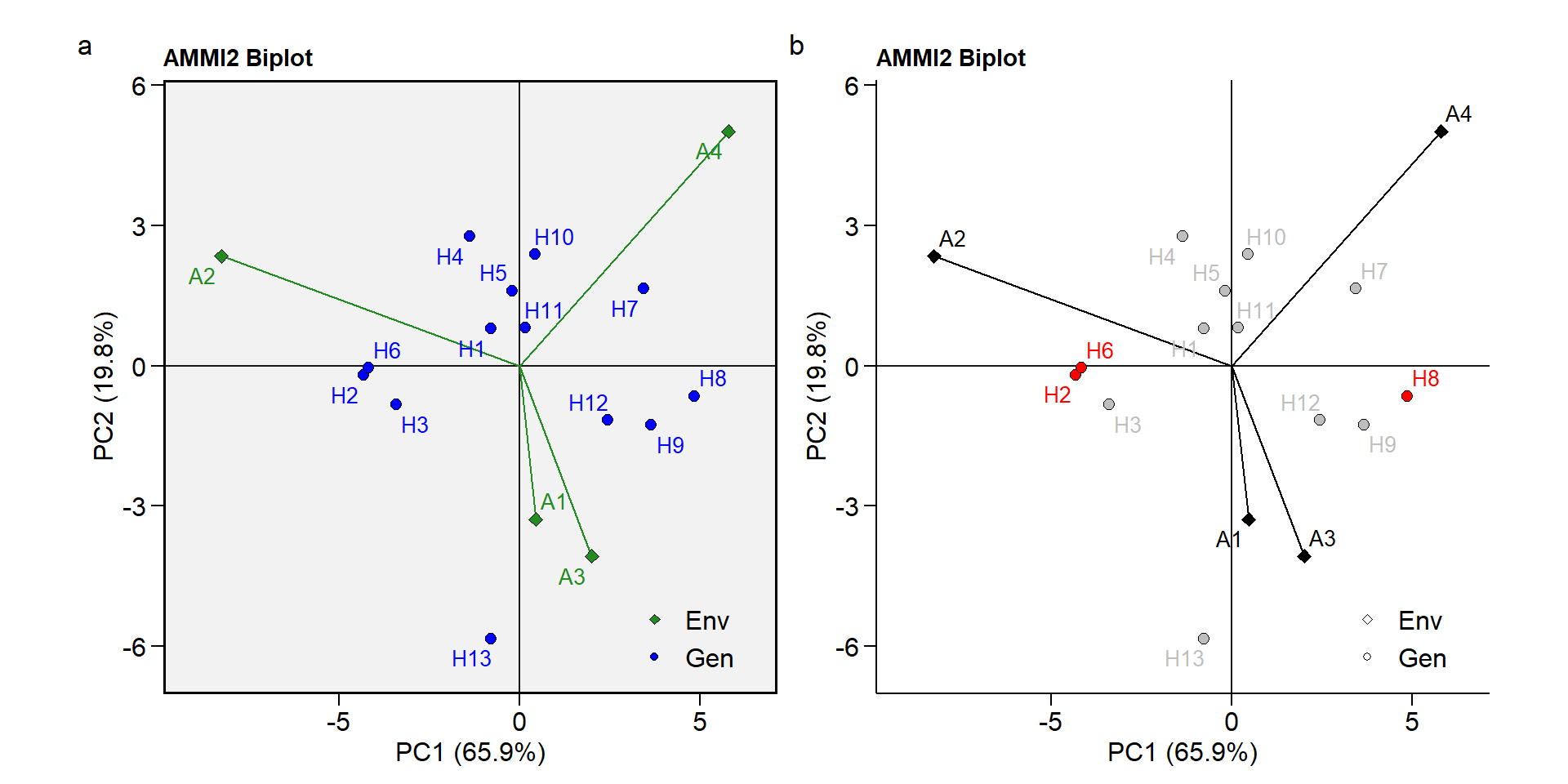
Temas

p <-
plot_scores(ammi_model,
            type = 2,
            col.segm.env = "black",
            col.gen = "gray",
            col.env = "black",
            highlight = c("H8", "H6", "H2"),
            col.highlight = "blue",
            size.tex.env = 5)

p1 <- p  + ggthemes::theme_base()
p2 <- p  + ggthemes::theme_clean()
p3 <- p  + ggthemes::theme_excel_new()
p4 <- p  + ggthemes::theme_solarized()
p5 <- p  + ggthemes::theme_solid()


arrange_ggplot((p1 + p2 + p3) / (p4 + p5),
               tag_levels = "i",
               tag_prefix = "p.",
               tag_suffix = ")",
               guides = "collect",
               title = "Meus biplots AMMI",
               subtitle = "Combinados no metan",
               caption = "Fonte: ...")