library(metan)
## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2
## |=========================================================|
## | Multi-Environment Trial Analysis (metan) v1.15.0        |
## | Author: Tiago Olivoto                                   |
## | Type 'citation('metan')' to know how to cite metan      |
## | Type 'vignette('metan_start')' for a short tutorial     |
## | Visit 'https://bit.ly/pkgmetan' for a complete tutorial |
## |=========================================================|
library(rio)
library(ggforce)
## Carregando pacotes exigidos: ggplot2

# gerar tabelas html
print_tbl <- function(table, digits = 3, ...){
  knitr::kable(table, booktabs = TRUE, digits = digits, ...)
}


df_ge <- import("http://bit.ly/df_ge", setclass = "tbl")

Índices univariados

A função waasb() calcula o WAASB, acrônimo para Weighted Average of the Absolute Scores obtidos pela decomposição por valores singulares dos BLUPs para interação genótipo-ambiente obtidos por um Modelo Linear de Efeito Misto¹. O índice WAASB para um determinado genótipo ((i\)) é dado por:

$$ WAASB_i = \sum_ {k = 1} ^ {p} | IPCA_ {ik} \times EP_k | / \sum_ {k = 1} ^ {p} EP_k $$

onde \(WAASB_i\) é a média ponderada dos scores absolutos do \(i\)-ésimo genótipo; \(IPCA_{ik}\) são os scores do \(i\)-ésimo genótipo no \(k\)-ésimo IPCA; \(EP_k\) é a variância explicada no \(k\)-ésimo IPCA para \(k = 1,2, .., p\), \(p = min (g-1; e-1)\). O modelo é ajustado com a função waasb(). Tanto waasb() quanto gamem_met() ajustam o mesmo modelo.

model_waasb <- 
  waasb(df_ge,
        env = ENV,
        gen = GEN,
        rep = BLOCO,
        resp = everything(), 
        verbose = FALSE)

# índice WAASB
waasb_ind <- gmd(model_waasb, "WAASB")
## Class of the model: waasb
## Variable extracted: WAASB
print_tbl(waasb_ind)

Biplots

Como o índice WAASB é baseado em decomposição por valores singulares, é possível obter os mesmos biplots utilizados na análise AMMI convencional

p1 <- plot_scores(model_waasb, var = 9)
p2 <- plot_scores(model_waasb, type = 2, var = 9)
p1 + p2

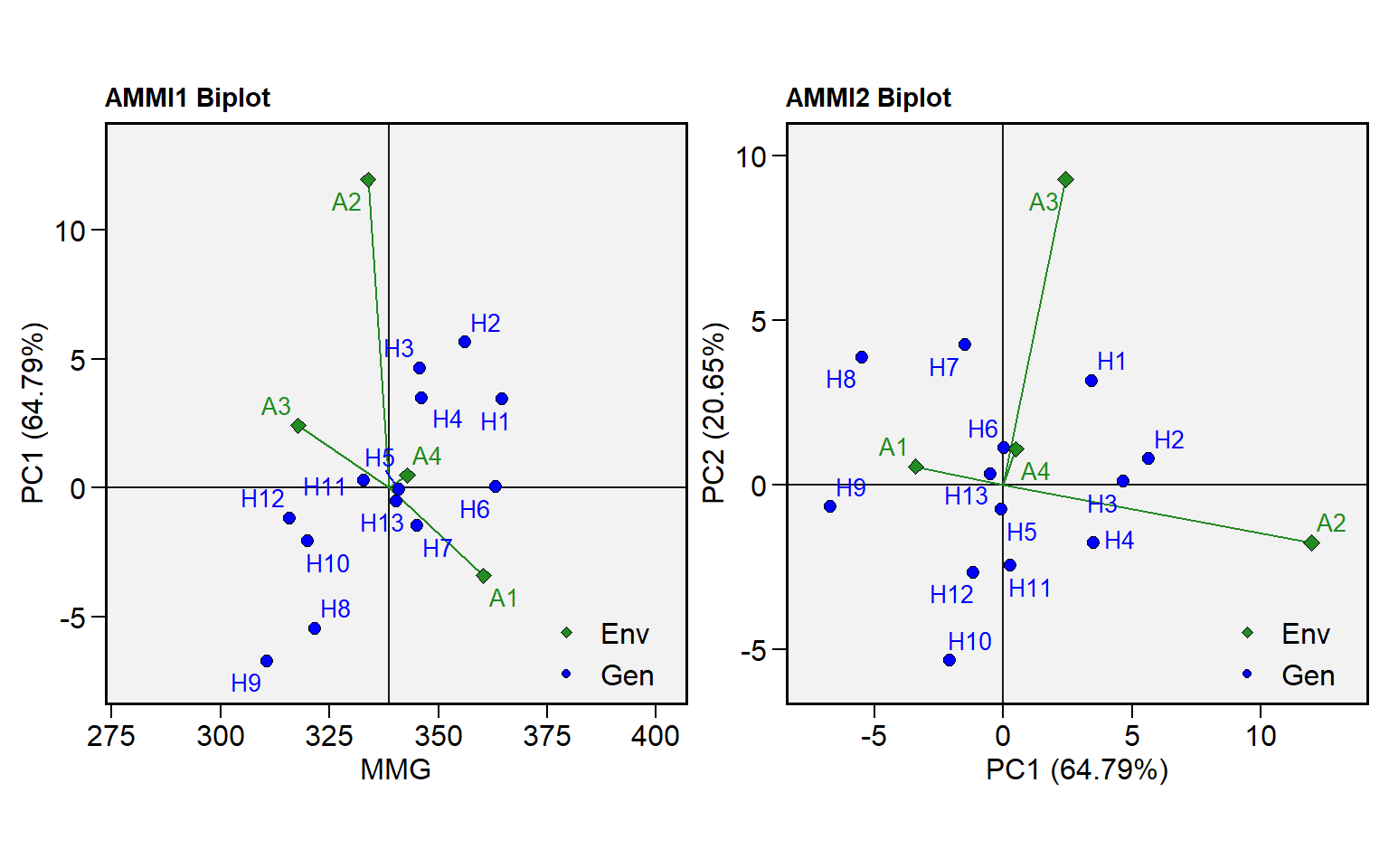
No método WAASB, o seguinte biplot representa quatro classificações relativas à interpretação conjunta de desempenho médio e estabilidade (para genótipos) ou discriminação (ambientes).

• Quadrante I. Os genótipos incluídos neste quadrante podem ser considerados genótipos instáveis e com produtividade abaixo da média geral. Ambientes neste quadrante apresentam alta capacidade de discriminação.

• Quadrante II. Neste quadrante estão incluídos os genótipos instáveis, embora com produtividade acima da média geral. Os ambientes incluídos neste quadrante merecem atenção especial, pois, além de proporcionarem altas magnitudes da variável resposta, apresentam boa capacidade de discriminação.

• Quadrante III. Os genótipos deste quadrante apresentam baixa produtividade, mas podem ser considerados estáveis, devido aos menores valores de WAASB. Quanto menor esse valor, mais estável o genótipo pode ser considerado. Os ambientes incluídos neste quadrante podem ser considerados pouco produtivos e com baixa capacidade de discriminação.

• Quadrante IV. Os genótipos dentro deste quadrante são altamente produtivos e amplamente adaptados devido à alta magnitude da variável de resposta e baixos valores do índice WAASB.

p3 <- plot_scores(model_waasb, type = 3, var = 9)
p4 <- plot_scores(model_waasb,
                  type = 3,
                  var = 9,
                  highlight = c("H1", "H6"),
                  plot_theme = theme_metan_minimal(),
                  title = FALSE)

arrange_ggplot(p3, p4, tag_levels = "a", guides = "collect")

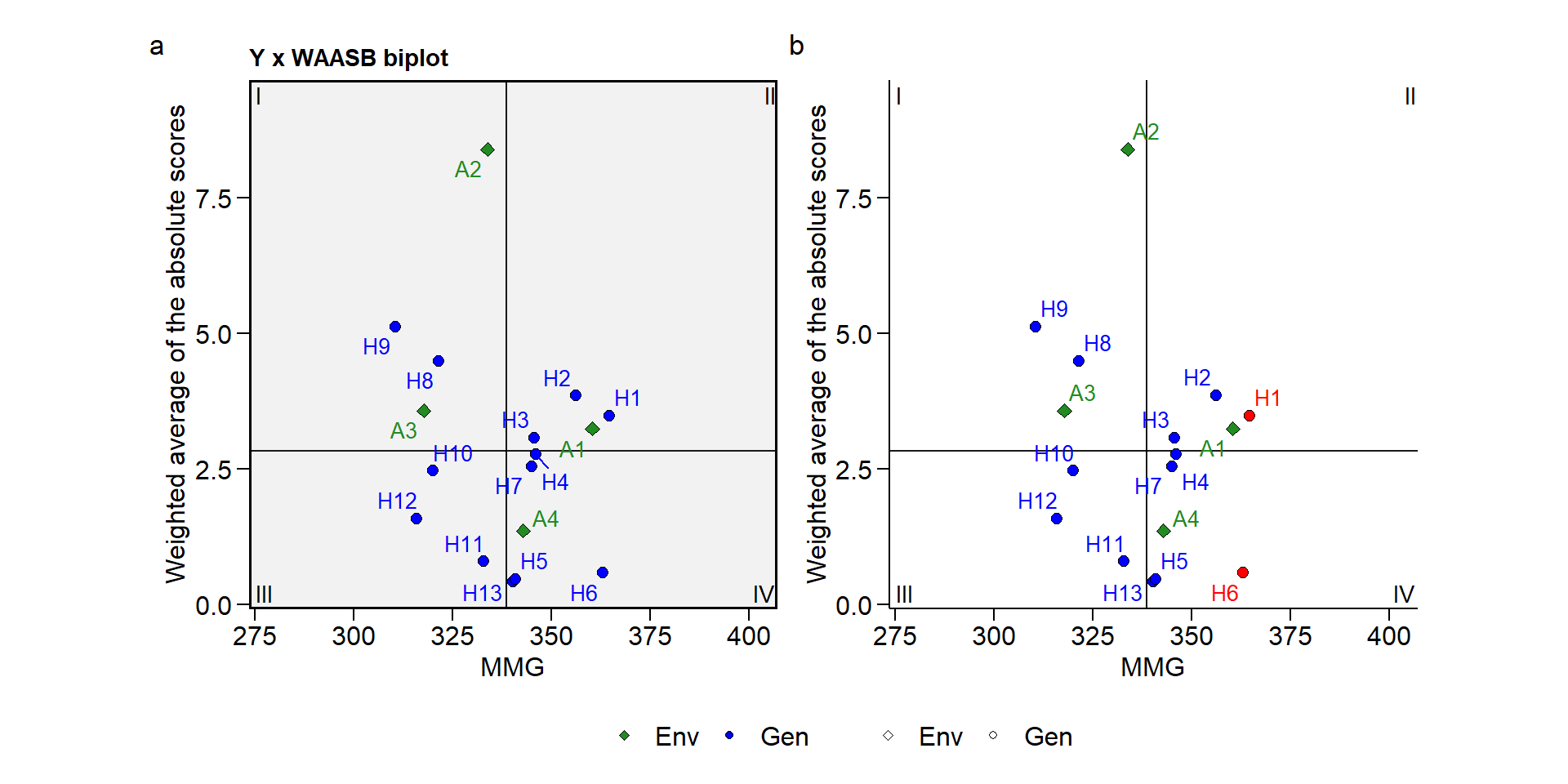
# extendendo o plot

desc <- c("Esses híbridos têm rendimento de grãos acima da média geral. \ N
Eles são mais estáveis do que aqueles acima da linha horizontal")
plot_scores(model_waasb,
            type = 3,
            var = 9, 
            x.lab = "Massa de mil grãos (g)",
            y.lab = "Média poderada dos escores absolutos (WAASB)",
            col.segm.env = "transparent") +
geom_mark_rect(aes(filter =  Code  %in% c("H13", "H4", "H6"),
                     label = "Descrição",
                     description = desc),
               label.fontsize = 9,
               show.legend = F,
               con.cap = 0,
               con.colour = "red",
               color = "red",
               expand = 0.015,
               label.buffer = unit(2, "cm"))+
theme_gray()+
theme(legend.position = c(0.1, 0.9),
      legend.background = element_blank(),
      legend.title = element_blank(),
      aspect.ratio = 1)

A seleção simultânea para desempenho médio e estabilidade é baseada no índice WAASBY¹. Este índice considera a estabilidade (WAASB) e o desempenho médio (variável dependente, Y) para classificação de genótipos considerando o seguinte modelo:

$$ WAASB{Y_i} = \frac {{\left ({r {G_i} \times {\theta _Y}} \right) + \left ({r {W_i} \times {\theta _S}} \right)}} {{{\theta _Y} + {\theta _S}}} $$

onde \(WAASBY_i\) é o índice de seleção simultânea para o \(i\)-ésimo genótipo que pondera entre desempenho e estabilidade; \(rY_i\) e \(rW_i\) são os valores reescalados (0-100) para a variável dependente e WAASB, respectivamente; \(\theta _Y\) e \(\theta_S\) são os pesos da variável dependente e WAASB, respectivamente. Os valores redimensionados são usados para tornar WAASB e Y diretamente comparáveis. Os valores máximo e mínimo para redimensionar a variável dependente dependerão do objetivo da seleção. Por exemplo, assumindo que o valor mais alto para a variável dependente é melhor, digamos, para rendimento de grãos, o genótipo com a média mais alta terá \(rY_i = 100\) após o reescalonamento. Por outro lado, se o valor mais baixo é melhor, digamos, para altura de espiga, o genótipo com a média mais baixa terá \(rY_i = 100\) após o reescalonamento. O genótipo com o menor WAASB terá \(rW_i = 100\). De fato, o índice WAASBY já é computado com a função waasb(), então, agora, basta extrair-mos os valores

waasby_ind <- gmd(model_waasb, what = "WAASBY")
## Class of the model: waasb
## Variable extracted: WAASBY
print_tbl(waasby_ind, digits = 2)

plot_waasby(model_waasb, var = "MMG")

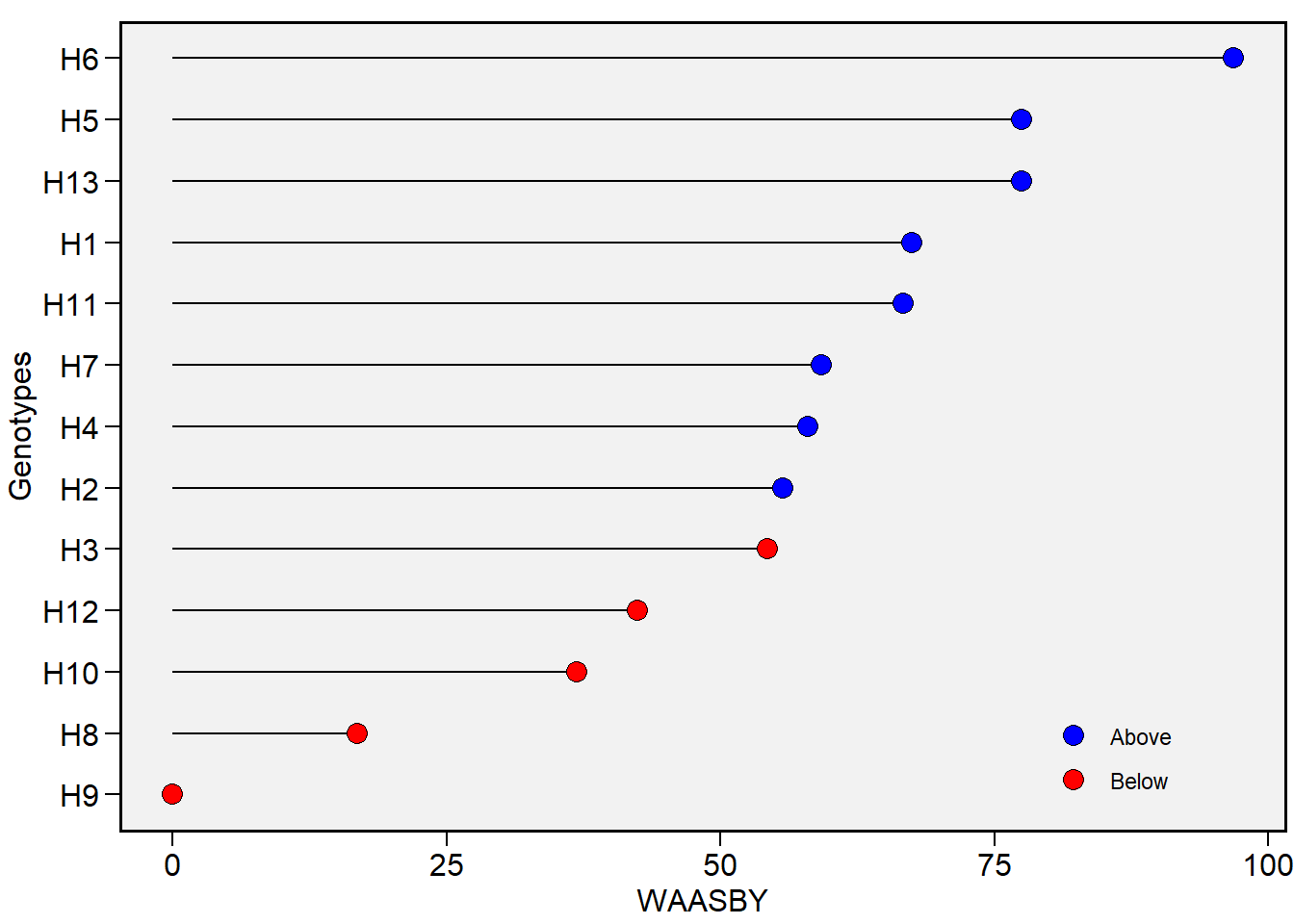
Índices multivariados

Índice de estabilidade multitrait (MTSI)

A função mtsi() é usada para calcular o índice de estabilidade multi-trait (MTSI)². Neste caso, com o modelo calculado com os argumentos padrões, todas as variáveis analizadas são para ter ganhos positivos desejados.

mtsi_model <- mtsi(model_waasb, verbose = FALSE)

# Autovalores e variância explicada
print_tbl(mtsi_model$PCA)

# Diferencial de seleção para estabilidade
print_tbl(mtsi_model$sel_dif_stab)

# Diferencial de seleção para performance
print_tbl(mtsi_model$sel_dif_trait)

Índice MGIDI

O índice MGIDI[] pode ser visto como o índice MTSI com um peso de 100 para o desempenho médio. Este índice é calculado com a função mgidi(). Aqui, usaremos os dados de exemplo df_g.

# dados
df_g <- import("http://bit.ly/df_g", setclass = "tbl")

gen_mod <- 
  gamem(df_g,
        gen = GEN,
        rep = BLOCO,
        resp = everything(),
        verbose = FALSE)


mgidi_mod <- mgidi(gen_mod)
## 
## -------------------------------------------------------------------------------
## Principal Component Analysis
## -------------------------------------------------------------------------------
## # A tibble: 10 x 4
##    PC    Eigenvalues `Variance (%)` `Cum. variance (%)`
##    <chr>       <dbl>          <dbl>               <dbl>
##  1 PC1          6.63          66.3                 66.3
##  2 PC2          1.59          15.9                 82.2
##  3 PC3          1.14          11.4                 93.6
##  4 PC4          0.46           4.6                 98.2
##  5 PC5          0.14           1.39                99.6
##  6 PC6          0.03           0.26                99.8
##  7 PC7          0.01           0.11                99.9
##  8 PC8          0.01           0.05               100. 
##  9 PC9          0              0.01               100  
## 10 PC10         0              0                  100  
## -------------------------------------------------------------------------------
## Factor Analysis - factorial loadings after rotation-
## -------------------------------------------------------------------------------
## # A tibble: 10 x 6
##    VAR         FA1   FA2   FA3 Communality Uniquenesses
##    <chr>     <dbl> <dbl> <dbl>       <dbl>        <dbl>
##  1 ALT_PLANT -0.83 -0.38  0.2         0.87         0.13
##  2 ALT_ESP   -0.84 -0.29  0.23        0.85         0.15
##  3 COMPES    -0.39 -0.92 -0.05        0.99         0.01
##  4 DIAMES    -0.84 -0.38  0.29        0.94         0.06
##  5 COMP_SAB  -0.88  0     0.18        0.8          0.2 
##  6 DIAM_SAB  -0.36 -0.91 -0.03        0.95         0.05
##  7 MGE       -0.74 -0.65  0           0.98         0.02
##  8 NFIL      -0.21 -0.08  0.97        0.99         0.01
##  9 MMG       -0.93 -0.28 -0.2         0.98         0.02
## 10 NGE       -0.04 -0.94  0.33        0.99         0.01
## -------------------------------------------------------------------------------
## Comunalit Mean: 0.9358222 
## -------------------------------------------------------------------------------
## Selection differential 
## -------------------------------------------------------------------------------
## # A tibble: 10 x 11
##    VAR      Factor     Xo     Xs     SD SDperc    h2     SG SGperc sense    goal
##    <chr>    <chr>   <dbl>  <dbl>  <dbl>  <dbl> <dbl>  <dbl>  <dbl> <chr>   <dbl>
##  1 ALT_PLA~ FA1      2.46   2.87  0.412  16.8  0.973  0.401  16.3  increa~   100
##  2 ALT_ESP  FA1      1.31   1.64  0.327  24.9  0.978  0.319  24.3  increa~   100
##  3 DIAMES   FA1     48.7   52.1   3.35    6.87 0.913  3.06    6.28 increa~   100
##  4 COMP_SAB FA1     28.5   29.7   1.26    4.43 0.942  1.19    4.17 increa~   100
##  5 MGE      FA1    168.   214.   45.3    26.9  0.933 42.2    25.1  increa~   100
##  6 MMG      FA1    334.   378.   43.7    13.1  0.929 40.6    12.2  increa~   100
##  7 COMPES   FA2     15.2   16.4   1.15    7.53 0.831  0.953   6.26 increa~   100
##  8 DIAM_SAB FA2     15.9   16.9   1.00    6.32 0.824  0.828   5.21 increa~   100
##  9 NGE      FA2    505.   556.   51.4    10.2  0.715 36.7     7.28 increa~   100
## 10 NFIL     FA3     15.8   16.9   1.10    6.97 0.784  0.863   5.47 increa~   100
## ------------------------------------------------------------------------------
## Selected genotypes
## -------------------------------------------------------------------------------
## H2 H6
## -------------------------------------------------------------------------------

# radar plot
plot(mgidi_mod)

# pontos fortes e fracos
plot(mgidi_mod, type = "contribution", genotypes = "all")

print_tbl(mgidi_mod$sel_dif)