Modelos biométricos
library(metan)
## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2
## |=========================================================|
## | Multi-Environment Trial Analysis (metan) v1.15.0 |
## | Author: Tiago Olivoto |
## | Type 'citation('metan')' to know how to cite metan |
## | Type 'vignette('metan_start')' for a short tutorial |
## | Visit 'https://bit.ly/pkgmetan' for a complete tutorial |
## |=========================================================|
library(rio)
# gerar tabelas html
print_tbl <- function(table, digits = 3, ...){
knitr::kable(table, booktabs = TRUE, digits = digits, ...)
}
df_ge <- import("http://bit.ly/df_ge", setclass = "tbl")
Correlação linear
A função corr_coef() pode ser usada para calcular o coeficiente de correlação de Pearson com valores de p. Um mapa de calor de correlação pode ser criado com a função plot().
# Todas as variáveis numéricas
ccoef <- corr_coef(df_ge)
plot(ccoef)
## Warning: Removed 5 rows containing missing values (geom_text).
Podemos usar uma função auxiliar de seleção para selecionar variáveis. Aqui, selecionaremos variáveis que começam com “C” ** OU ** termina com “D” usando union_var ().
ccoef2 <- corr_coef(df_ge, contains("A"))
plot(ccoef2, dígitos = 2)
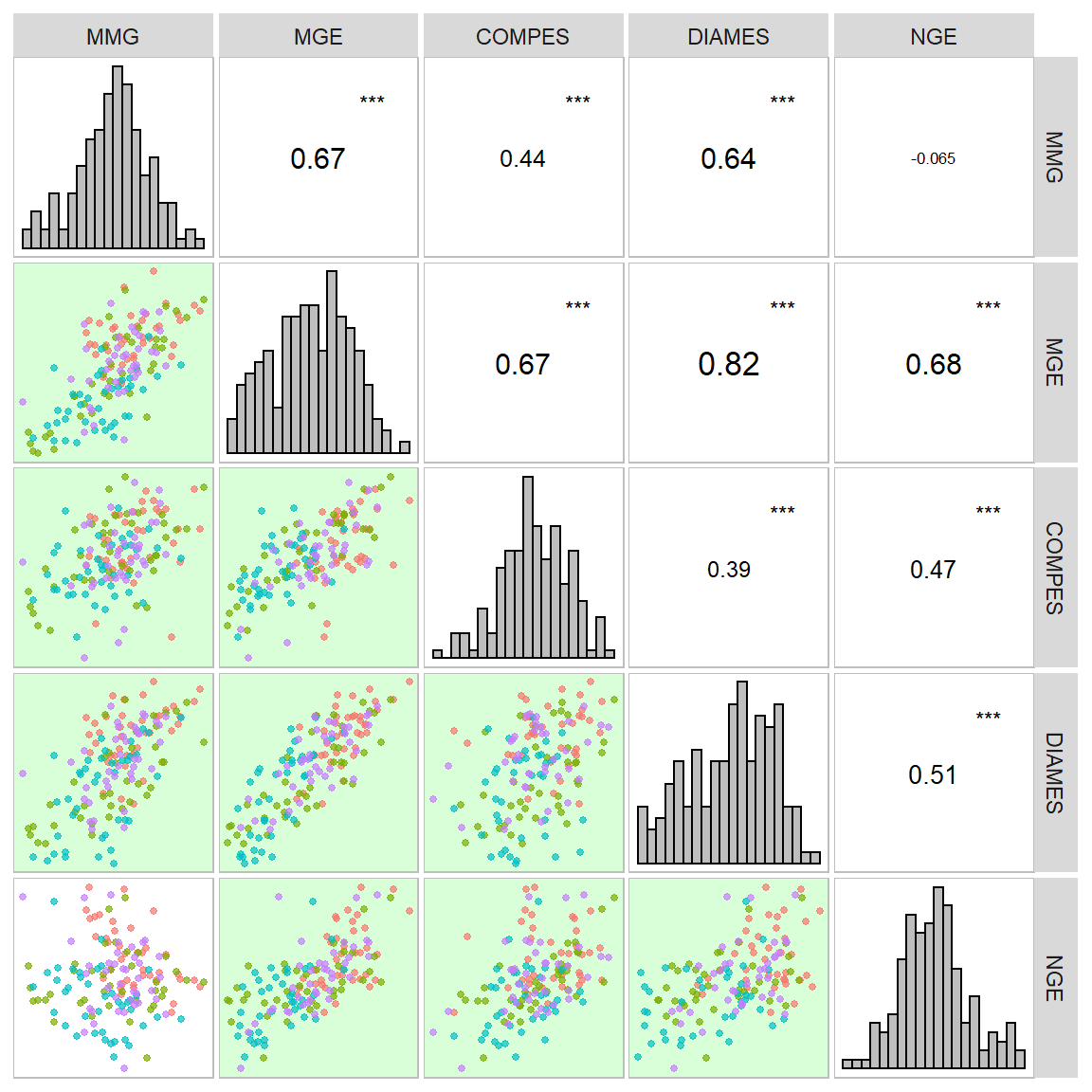
A função corr_plot() pode ser usada para visualizar (graficamente e numericamente) uma matriz de correlação. Os gráficos de dispersão em pares são produzidos e podem ser mostrados na diagonal superior ou inferior, o que pode ser visto como uma versão mais agradável e personalizável baseada em ggplot2 da função R de base de pairs().
a <- corr_plot(df_ge, MMG, MGE, COMPES, DIAMES, NGE)
corr_plot(df_ge, MMG, MGE, COMPES, DIAMES, NGE,
lower = NULL,
upper = "corr")
corr_plot(df_ge, MMG, MGE, COMPES, DIAMES, NGE,
shape.point = 19,
size.point = 2,
alpha.point = 0.5,
alpha.diag = 0,
pan.spacing = 0,
diag.type = "boxplot",
col.sign = "gray",
alpha.sign = 0.3,
axis.labels = TRUE)
corr_plot(df_ge, MMG, MGE, COMPES, DIAMES, NGE,
prob = 0.01,
shape.point = 21,
col.point = "black",
fill.point = "orange",
size.point = 2,
alpha.point = 0.6,
maxsize = 4,
minsize = 2,
smooth = TRUE,
size.smooth = 1,
col.smooth = "black",
col.sign = "cyan",
col.up.panel = "black",
col.lw.panel = "black",
col.dia.panel = "black",
pan.spacing = 0,
lab.position = "tl")
Também é possível usar uma variável categórica dos dados para mapear o gráfico de dispersão por cores.
corr_plot(df_ge, MMG, MGE, COMPES, DIAMES, NGE, col.by = ENV)
Matrizes de correlação/covariância
A função covcor_design() pode ser usada para calcular matrizes de correlação genéticas, fenotípicas e residuais de correlação por meio da Análise de Variância (ANOVA) usando um delineamento de bloco completo ao acaso (DBC) ou delineamento inteiramente ao acaso (DIC).
As correlações fenotípicas (\(r_p\)), genotípicas (\(r_g\)) e residuais (\(r_r\)) são calculadas da seguinte forma:
$$
r ^ p_ {xy} = \frac {cov ^ p_ {xy}} {\sqrt {var ^ p_ {x} var ^ p_ {y}}} \
r ^ g_ {xy} = \frac {cov ^ g_ {xy}} {\sqrt {var ^ g_ {x} var ^ g_ {y}}} \
r ^ r_ {xy} = \frac {cov ^ r_ {xy}} {\sqrt {var ^ r_ {x} var ^ r_ {y}}}
$$
Usando os quadrados médios (MS) do método ANOVA, as variâncias (var) e as covariâncias (cov) são calculadas da seguinte forma:
$$
cov ^ p_ {xy} = [(MST_ {x + y} - MST_x - MST_y) / 2] / r \
var ^ p_x = MST_x / r \
var ^ p_y = MST_y / r \
cov ^ r_ {xy} = (MSR_ {x + y} - MSR_x - MSR_y) / 2 \
var ^ r_x = MSR_x \
var ^ r_y = MSR_y \
cov ^ g_ {xy} = [(cov ^ p_ {xy} \times r) - cov ^ r_ {xy}] / r \
var ^ g_x = (MST_x - MSE_x) / r \
var ^ g_y = (MST_x - MSE_y) / r \
$$
onde \(MST\) é o quadrado médio para tratamento, \(MSR\) é o quadrado médio para resíduos e \(r\) é o número de repetições. A função covcor_design() retorna uma lista com as matrize. Matrizes específicas podem ser retornadas usando o argumento type, conforme mostrado abaixo.
df_g <- import("http://bit.ly/df_g", setclass = "tbl")
correl <- covcor_design(df_g,
gen = GEN,
rep = BLOCO,
resp = c(MMG, MGE, COMPES, DIAMES, NGE))
Correlações
# genéticas
print_tbl(correl$geno_cor)
| MMG | MGE | COMPES | DIAMES | NGE | |
|---|---|---|---|---|---|
| MMG | 1.000 | 0.927 | 0.671 | 0.906 | 0.368 |
| MGE | 0.927 | 1.000 | 0.918 | 0.933 | 0.692 |
| COMPES | 0.671 | 0.918 | 1.000 | 0.752 | 0.992 |
| DIAMES | 0.906 | 0.933 | 0.752 | 1.000 | 0.561 |
| NGE | 0.368 | 0.692 | 0.992 | 0.561 | 1.000 |
# fenotípicas
print_tbl(correl$phen_cor)
| MMG | MGE | COMPES | DIAMES | NGE | |
|---|---|---|---|---|---|
| MMG | 1.000 | 0.893 | 0.628 | 0.852 | 0.241 |
| MGE | 0.893 | 1.000 | 0.883 | 0.897 | 0.651 |
| COMPES | 0.628 | 0.883 | 1.000 | 0.661 | 0.854 |
| DIAMES | 0.852 | 0.897 | 0.661 | 1.000 | 0.496 |
| NGE | 0.241 | 0.651 | 0.854 | 0.496 | 1.000 |
# residuais
print_tbl(correl$resi_cor)
| MMG | MGE | COMPES | DIAMES | NGE | |
|---|---|---|---|---|---|
| MMG | 1.000 | 0.431 | 0.348 | 0.223 | -0.417 |
| MGE | 0.431 | 1.000 | 0.704 | 0.466 | 0.624 |
| COMPES | 0.348 | 0.704 | 1.000 | 0.050 | 0.408 |
| DIAMES | 0.223 | 0.466 | 0.050 | 1.000 | 0.275 |
| NGE | -0.417 | 0.624 | 0.408 | 0.275 | 1.000 |
Covariâncias
# genéticas
print_tbl(correl$geno_cov)
| MMG | MGE | COMPES | DIAMES | NGE | |
|---|---|---|---|---|---|
| MMG | 2941.365 | 1721.242 | 39.930 | 120.289 | 819.553 |
| MGE | 1721.242 | 1172.429 | 34.496 | 78.218 | 971.370 |
| COMPES | 39.930 | 34.496 | 1.205 | 2.020 | 44.672 |
| DIAMES | 120.289 | 78.218 | 2.020 | 5.992 | 56.286 |
| NGE | 819.553 | 971.370 | 44.672 | 56.286 | 1682.787 |
# fenotípicas
print_tbl(correl$phen_cov)
| MMG | MGE | COMPES | DIAMES | NGE | |
|---|---|---|---|---|---|
| MMG | 3165.893 | 1780.539 | 42.506 | 122.810 | 657.574 |
| MGE | 1780.539 | 1256.627 | 37.692 | 81.442 | 1119.668 |
| COMPES | 42.506 | 37.692 | 1.449 | 2.038 | 49.899 |
| DIAMES | 122.810 | 81.442 | 2.038 | 6.560 | 61.649 |
| NGE | 657.574 | 1119.668 | 49.899 | 61.649 | 2354.128 |
# residuais
print_tbl(correl$resi_cov)
| MMG | MGE | COMPES | DIAMES | NGE | |
|---|---|---|---|---|---|
| MMG | 673.583 | 177.892 | 7.730 | 7.564 | -485.939 |
| MGE | 177.892 | 252.595 | 9.588 | 9.672 | 444.893 |
| COMPES | 7.730 | 9.588 | 0.734 | 0.056 | 15.681 |
| DIAMES | 7.564 | 9.672 | 0.056 | 1.703 | 16.090 |
| NGE | -485.939 | 444.893 | 15.681 | 16.090 | 2014.021 |
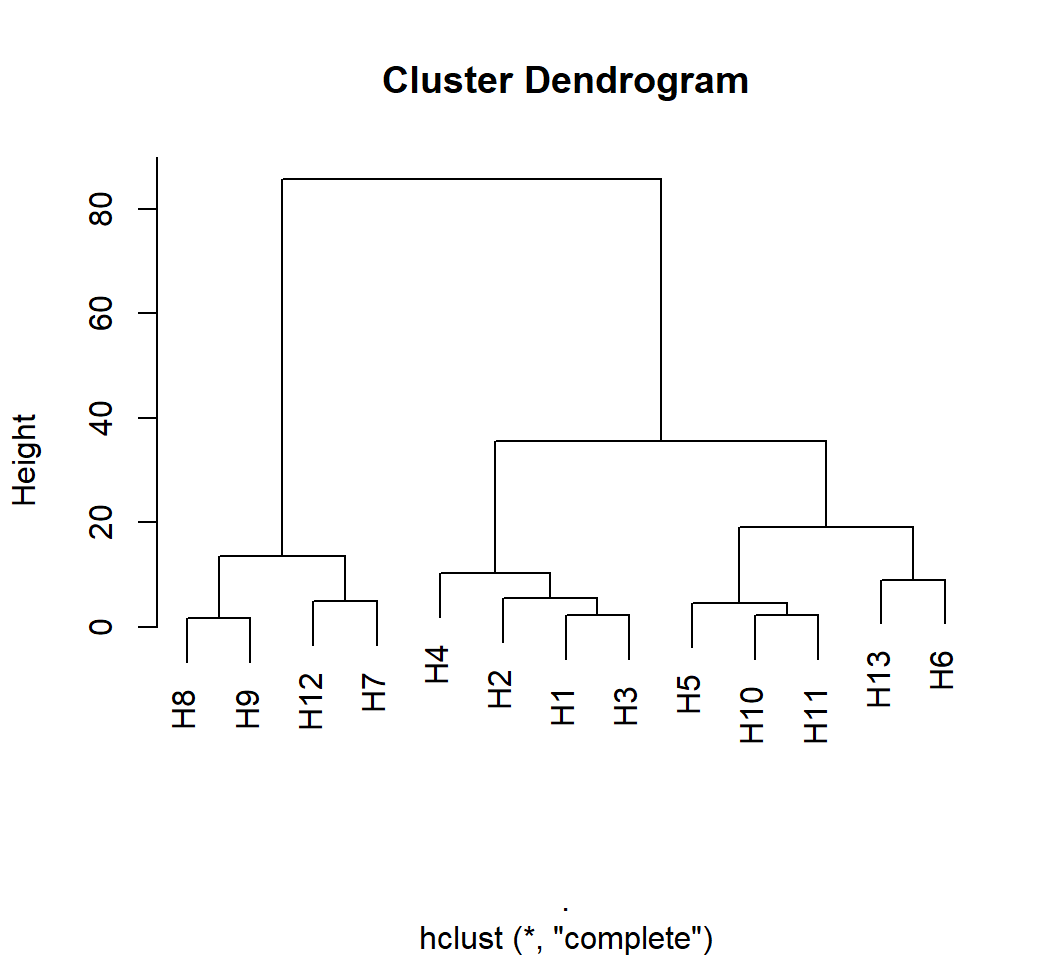
Distância de Mahalanobis
A matriz de covariância residual e as médias podem ser usados na função mahala() para calcular a distância de Mahalanobis.
D2 <- mahala(.means = correl$means, covar = correl$resi_cov, inverted = FALSE)
print_tbl(D2)
| H1 | H10 | H11 | H12 | H13 | H2 | H3 | H4 | H5 | H6 | H7 | H8 | H9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H1 | 0.000 | 22.376 | 14.474 | 23.648 | 12.483 | 3.844 | 2.334 | 7.508 | 17.464 | 14.837 | 26.980 | 59.690 | 51.562 |
| H10 | 22.376 | 0.000 | 2.334 | 8.772 | 9.100 | 35.607 | 18.127 | 10.696 | 2.903 | 18.311 | 5.290 | 18.563 | 13.522 |
| H11 | 14.474 | 2.334 | 0.000 | 5.474 | 10.975 | 25.937 | 9.655 | 6.592 | 4.653 | 19.124 | 6.482 | 23.686 | 19.195 |
| H12 | 23.648 | 8.772 | 5.474 | 0.000 | 18.393 | 42.726 | 20.782 | 22.110 | 17.671 | 37.538 | 4.956 | 13.675 | 10.465 |
| H13 | 12.483 | 9.100 | 10.975 | 18.393 | 0.000 | 23.219 | 16.462 | 11.848 | 7.893 | 9.072 | 10.616 | 30.521 | 24.450 |
| H2 | 3.844 | 35.607 | 25.937 | 42.726 | 23.219 | 0.000 | 5.541 | 10.274 | 24.275 | 14.521 | 44.357 | 85.575 | 77.169 |
| H3 | 2.334 | 18.127 | 9.655 | 20.782 | 16.462 | 5.541 | 0.000 | 3.420 | 13.807 | 16.940 | 26.131 | 58.552 | 50.893 |
| H4 | 7.508 | 10.696 | 6.592 | 22.110 | 11.848 | 10.274 | 3.420 | 0.000 | 5.399 | 9.827 | 21.315 | 51.358 | 44.707 |
| H5 | 17.464 | 2.903 | 4.653 | 17.671 | 7.893 | 24.275 | 13.807 | 5.399 | 0.000 | 7.806 | 11.084 | 31.217 | 25.982 |
| H6 | 14.837 | 18.311 | 19.124 | 37.538 | 9.072 | 14.521 | 16.940 | 9.827 | 7.806 | 0.000 | 25.371 | 54.420 | 49.052 |
| H7 | 26.980 | 5.290 | 6.482 | 4.956 | 10.616 | 44.357 | 26.131 | 21.315 | 11.084 | 25.371 | 0.000 | 6.956 | 6.100 |
| H8 | 59.690 | 18.563 | 23.686 | 13.675 | 30.521 | 85.575 | 58.552 | 51.358 | 31.217 | 54.420 | 6.956 | 0.000 | 1.796 |
| H9 | 51.562 | 13.522 | 19.195 | 10.465 | 24.450 | 77.169 | 50.893 | 44.707 | 25.982 | 49.052 | 6.100 | 1.796 | 0.000 |
D2 %>%
as.dist() %>%
hclust() %>%
plot()
Diagnóstico de colinearidade
Os códigos a seguir calculam um diagnóstico de colinearidade completo de uma matriz de correlação de características do preditor. Vários indicadores, como fator de inflação de variância, número de condição e determinante da matriz são considerados1
colin <- colindiag(df_ge)
print(colin)
## The multicollinearity in the matrix should be investigated.
## CN = 607.708
## Largest VIF = 55.4696961923099
## Matrix determinant: 1.7e-06
## Largest correlation: ALT_PLANT x ALT_ESP = 0.932
## Smallest correlation: COMPES x NFIL = -0.014
## Number of VIFs > 10: 4
## Number of correlations with r >= |0.8|: 3
## Variables with largest weight in the last eigenvalues:
## MGE > NGE > MMG > ALT_ESP > ALT_PLANT > DIAMES > DIAM_SAB > NFIL > COMPES > COMP_SAB
print_tbl(colin$evalevet)
| Eigenvalues | ALT_PLANT | ALT_ESP | COMPES | DIAMES | COMP_SAB | DIAM_SAB | MGE | NFIL | MMG | NGE |
|---|---|---|---|---|---|---|---|---|---|---|
| 5.275 | -0.358 | -0.346 | -0.297 | -0.382 | -0.263 | -0.283 | -0.416 | -0.178 | -0.306 | -0.265 |
| 1.669 | 0.106 | 0.066 | -0.311 | 0.137 | -0.119 | -0.344 | 0.012 | 0.634 | -0.398 | 0.420 |
| 1.448 | -0.163 | -0.219 | 0.464 | -0.201 | -0.389 | 0.452 | 0.085 | -0.010 | -0.335 | 0.440 |
| 0.914 | 0.498 | 0.487 | -0.049 | -0.260 | -0.568 | -0.163 | 0.035 | -0.306 | 0.000 | 0.011 |
| 0.294 | -0.155 | -0.419 | -0.208 | 0.301 | -0.474 | -0.194 | 0.421 | -0.105 | 0.447 | 0.128 |
| 0.179 | -0.175 | 0.111 | -0.190 | 0.012 | 0.370 | -0.215 | 0.221 | -0.615 | -0.249 | 0.498 |
| 0.092 | 0.194 | -0.054 | -0.504 | 0.465 | -0.120 | 0.574 | -0.239 | -0.197 | -0.220 | -0.033 |
| 0.073 | -0.216 | 0.201 | 0.457 | 0.644 | -0.197 | -0.317 | -0.250 | -0.151 | -0.216 | -0.135 |
| 0.047 | 0.668 | -0.598 | 0.237 | 0.064 | 0.164 | -0.237 | -0.120 | -0.147 | -0.124 | 0.042 |
| 0.009 | 0.033 | -0.038 | -0.009 | 0.024 | 0.006 | 0.019 | 0.677 | 0.011 | -0.514 | -0.523 |
Diagnóstico para cada nível do fator ENV
colin2 <- colindiag(df_ge, by = ENV)
print(colin2)
## # A tibble: 4 x 2
## ENV data
## <chr> <list>
## 1 A1 <colindig>
## 2 A2 <colindig>
## 3 A3 <colindig>
## 4 A4 <colindig>
Análise de trilha
Neste exemplo, a variável massa de grãos por espiga (MGE) será utilziada como resposta e todas as outras como explicativa
pcoeff <- path_coeff(df_ge, resp = MGE)
## Weak multicollinearity.
## Condition Number = 97.581
## You will probably have path coefficients close to being unbiased.
print(pcoeff)
## ----------------------------------------------------------------------------------------------
## Correlation matrix between the predictor traits
## ----------------------------------------------------------------------------------------------
## ALT_PLANT ALT_ESP COMPES DIAMES COMP_SAB DIAM_SAB NFIL MMG
## ALT_PLANT 1.0000 0.9318 0.38020 0.6613 0.32516 0.31539 0.32861 0.56854
## ALT_ESP 0.9318 1.0000 0.36265 0.6303 0.39719 0.28051 0.26481 0.56236
## COMPES 0.3802 0.3627 1.00000 0.3851 0.25541 0.91187 -0.01387 0.44210
## DIAMES 0.6613 0.6303 0.38515 1.0000 0.69746 0.38971 0.55253 0.64199
## COMP_SAB 0.3252 0.3972 0.25541 0.6975 1.00000 0.30036 0.26194 0.61870
## DIAM_SAB 0.3154 0.2805 0.91187 0.3897 0.30036 1.00000 -0.03585 0.44332
## NFIL 0.3286 0.2648 -0.01387 0.5525 0.26194 -0.03585 1.00000 -0.10876
## MMG 0.5685 0.5624 0.44210 0.6420 0.61870 0.44332 -0.10876 1.00000
## NGE 0.4584 0.3881 0.46570 0.5051 0.04894 0.41562 0.62609 -0.06516
## NGE
## ALT_PLANT 0.45838
## ALT_ESP 0.38812
## COMPES 0.46570
## DIAMES 0.50508
## COMP_SAB 0.04894
## DIAM_SAB 0.41562
## NFIL 0.62609
## MMG -0.06516
## NGE 1.00000
## ----------------------------------------------------------------------------------------------
## Vector of correlations between dependent and each predictor
## ----------------------------------------------------------------------------------------------
## ALT_PLANT ALT_ESP COMPES DIAMES COMP_SAB DIAM_SAB NFIL
## MGE 0.7534439 0.7029469 0.6685601 0.8241426 0.470931 0.6259806 0.3621447
## MMG NGE
## MGE 0.6730371 0.6810756
## ----------------------------------------------------------------------------------------------
## Multicollinearity diagnosis and goodness-of-fit
## ----------------------------------------------------------------------------------------------
## Condition number: 97.5813
## Determinant: 9.241e-05
## R-square: 0.982
## Residual: 0.1343
## Response: MGE
## Predictors: ALT_PLANT ALT_ESP COMPES DIAMES COMP_SAB DIAM_SAB NFIL MMG NGE
## ----------------------------------------------------------------------------------------------
## Variance inflation factors
## ----------------------------------------------------------------------------------------------
## # A tibble: 9 x 2
## VAR VIF
## <chr> <dbl>
## 1 ALT_PLANT 11.30
## 2 ALT_ESP 9.302
## 3 COMPES 7.331
## 4 DIAMES 8.636
## 5 COMP_SAB 3.270
## 6 DIAM_SAB 6.814
## 7 NFIL 3.676
## 8 MMG 6.965
## 9 NGE 5.396
## ----------------------------------------------------------------------------------------------
## Eigenvalues and eigenvectors
## ----------------------------------------------------------------------------------------------
## # A tibble: 9 x 10
## Eigenvalues ALT_PLANT ALT_ESP COMPES DIAMES COMP_SAB DIAM_SAB NFIL
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 4.382 -0.3957 -0.3860 -0.3207 -0.4210 -0.3025 -0.3069 -0.1968
## 2 1.669 -0.1105 -0.07139 0.3116 -0.1422 0.1131 0.3450 -0.6359
## 3 1.436 -0.1416 -0.1977 0.4834 -0.1783 -0.3687 0.4719 0.01084
## 4 0.9130 0.5057 0.4952 -0.03763 -0.2558 -0.5642 -0.1520 -0.3006
## 5 0.2429 0.03453 0.3984 0.1010 -0.4234 0.5823 0.05879 -0.06332
## 6 0.1638 -0.1483 0.01160 -0.2195 0.2790 0.1830 -0.1836 -0.6531
## 7 0.08619 -0.2376 0.08451 0.6328 -0.1318 0.03175 -0.6776 0.06203
## 8 0.06259 -0.2610 0.3031 0.2035 0.6326 -0.2275 -0.01768 -0.09131
## 9 0.04490 0.6385 -0.5511 0.2544 0.1748 0.1271 -0.2106 -0.1540
## # ... with 2 more variables: MMG <dbl>, NGE <dbl>
## ----------------------------------------------------------------------------------------------
## Variables with the largest weight in the eigenvalue of smallest magnitude
## ----------------------------------------------------------------------------------------------
## ALT_PLANT > ALT_ESP > MMG > COMPES > DIAM_SAB > DIAMES > NFIL > NGE > COMP_SAB
## ----------------------------------------------------------------------------------------------
## Direct (diagonal) and indirect (off-diagonal) effects
## ----------------------------------------------------------------------------------------------
## ALT_PLANT ALT_ESP COMPES DIAMES COMP_SAB
## ALT_PLANT -0.013315310 0.04002135 0.0138641226 0.015196362 -0.0047188442
## ALT_ESP -0.012407581 0.04294928 0.0132244307 0.014482662 -0.0057641364
## COMPES -0.005062428 0.01557572 0.0364657233 0.008850255 -0.0037065040
## DIAMES -0.008805612 0.02706905 0.0140445955 0.022979012 -0.0101216939
## COMP_SAB -0.004329670 0.01705918 0.0093135921 0.016027009 -0.0145121611
## DIAM_SAB -0.004199528 0.01204778 0.0332518264 0.008955216 -0.0043589255
## NFIL -0.004375497 0.01137319 -0.0005059176 0.012696697 -0.0038012563
## MMG -0.007570266 0.02415282 0.0161215357 0.014752226 -0.0089786759
## NGE -0.006103472 0.01666954 0.0169820638 0.011606259 -0.0007102577
## DIAM_SAB NFIL MMG NGE linear
## ALT_PLANT -0.0067498812 -0.0082032241 0.3909975 0.32635179 0.7534439
## ALT_ESP -0.0060034106 -0.0066105076 0.3867462 0.27632993 0.7029469
## COMPES -0.0195154051 0.0003463406 0.3040435 0.33156290 0.6685601
## DIAMES -0.0083404905 -0.0137932898 0.4415098 0.35960124 0.8241426
## COMP_SAB -0.0064282721 -0.0065388826 0.4254949 0.03484530 0.4709310
## DIAM_SAB -0.0214016323 0.0008949437 0.3048852 0.29590577 0.6259806
## NFIL 0.0007672451 -0.0249636726 -0.0747987 0.44575261 0.3621447
## MMG -0.0094878766 0.0027151156 0.6877240 -0.04639172 0.6730371
## NGE -0.0088948788 -0.0156293919 -0.0448120 0.71196770 0.6810756
## ----------------------------------------------------------------------------------------------
Para declarar características preditoras, use o argumento pred
pcoeff2 <-
path_coeff(df_ge,
resp = MGE,
pred = c(MMG, COMPES, DIAMES, NGE))
## Weak multicollinearity.
## Condition Number = 24.907
## You will probably have path coefficients close to being unbiased.
print(pcoeff2)
## ----------------------------------------------------------------------------------------------
## Correlation matrix between the predictor traits
## ----------------------------------------------------------------------------------------------
## MMG COMPES DIAMES NGE
## MMG 1.00000 0.4421 0.6420 -0.06516
## COMPES 0.44210 1.0000 0.3851 0.46570
## DIAMES 0.64199 0.3851 1.0000 0.50508
## NGE -0.06516 0.4657 0.5051 1.00000
## ----------------------------------------------------------------------------------------------
## Vector of correlations between dependent and each predictor
## ----------------------------------------------------------------------------------------------
## MMG COMPES DIAMES NGE
## MGE 0.6730371 0.6685601 0.8241426 0.6810756
## ----------------------------------------------------------------------------------------------
## Multicollinearity diagnosis and goodness-of-fit
## ----------------------------------------------------------------------------------------------
## Condition number: 24.9068
## Determinant: 0.1311275
## R-square: 0.981
## Residual: 0.1379
## Response: MGE
## Predictors: MMG COMPES DIAMES NGE
## ----------------------------------------------------------------------------------------------
## Variance inflation factors
## ----------------------------------------------------------------------------------------------
## # A tibble: 4 x 2
## VAR VIF
## <chr> <dbl>
## 1 MMG 4.277
## 2 COMPES 2.183
## 3 DIAMES 4.245
## 4 NGE 3.529
## ----------------------------------------------------------------------------------------------
## Eigenvalues and eigenvectors
## ----------------------------------------------------------------------------------------------
## # A tibble: 4 x 5
## Eigenvalues MMG COMPES DIAMES NGE
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2.217 -0.4726 -0.5146 -0.5837 -0.4137
## 2 1.077 -0.6640 0.1302 -0.09487 0.7302
## 3 0.6170 -0.02383 -0.7914 0.5790 0.1947
## 4 0.08902 0.5790 -0.3032 -0.5613 0.5076
## ----------------------------------------------------------------------------------------------
## Variables with the largest weight in the eigenvalue of smallest magnitude
## ----------------------------------------------------------------------------------------------
## MMG > DIAMES > NGE > COMPES
## ----------------------------------------------------------------------------------------------
## Direct (diagonal) and indirect (off-diagonal) effects
## ----------------------------------------------------------------------------------------------
## MMG COMPES DIAMES NGE linear
## MMG 0.7207458 0.007125379 -0.007499726 -0.04733433 0.6730371
## COMPES 0.3186425 0.016117081 -0.004499286 0.33829981 0.6685601
## DIAMES 0.4627094 0.006207415 -0.011682054 0.36690786 0.8241426
## NGE -0.0469637 0.007505714 -0.005900382 0.72643393 0.6810756
## ----------------------------------------------------------------------------------------------
Para selecionando um conjunto de preditores com multicolinearidade mínima use o argumento brutstep.
pcoeff3 <-
path_coeff(df_ge,
resp = MGE,
brutstep = TRUE)
## --------------------------------------------------------------------------
## The algorithm has selected a set of 8 predictors with largest VIF = 8.634.
## Selected predictors: ALT_ESP COMP_SAB NFIL NGE MMG DIAM_SAB COMPES DIAMES
## A forward stepwise-based selection procedure will fit 6 models.
## --------------------------------------------------------------------------
## Adjusting the model 1 with 7 predictors (16.67% concluded)
## Adjusting the model 2 with 6 predictors (33.33% concluded)
## Adjusting the model 3 with 5 predictors (50% concluded)
## Adjusting the model 4 with 4 predictors (66.67% concluded)
## Adjusting the model 5 with 3 predictors (83.33% concluded)
## Adjusting the model 6 with 2 predictors (100% concluded)
## Done!
## --------------------------------------------------------------------------
## Summary of the adjusted models
## --------------------------------------------------------------------------
## Model AIC Numpred CN Determinant R2 Residual maxVIF
## MODEL_1 923 7 51.94 0.00291 0.982 0.135 7.21
## MODEL_2 921 6 42.05 0.01919 0.982 0.135 6.61
## MODEL_3 921 5 34.25 0.06367 0.982 0.136 5.15
## MODEL_4 924 4 24.91 0.13113 0.981 0.138 4.28
## MODEL_5 1234 3 4.00 0.56087 0.860 0.375 1.52
## MODEL_6 1267 2 2.25 0.85166 0.824 0.420 1.17
## --------------------------------------------------------------------------
print(pcoeff3$Models$Model_4)
## ----------------------------------------------------------------------------------------------
## Correlation matrix between the predictor traits
## ----------------------------------------------------------------------------------------------
## DIAMES COMPES NGE MMG
## DIAMES 1.0000 0.3851 0.50508 0.64199
## COMPES 0.3851 1.0000 0.46570 0.44210
## NGE 0.5051 0.4657 1.00000 -0.06516
## MMG 0.6420 0.4421 -0.06516 1.00000
## ----------------------------------------------------------------------------------------------
## Vector of correlations between dependent and each predictor
## ----------------------------------------------------------------------------------------------
## DIAMES COMPES NGE MMG
## MGE 0.8241426 0.6685601 0.6810756 0.6730371
## ----------------------------------------------------------------------------------------------
## Multicollinearity diagnosis and goodness-of-fit
## ----------------------------------------------------------------------------------------------
## Condition number: 24.9068
## Determinant: 0.1311275
## R-square: 0.981
## Residual: 0.1379
## Response: MGE
## Predictors: DIAMES COMPES NGE MMG
## ----------------------------------------------------------------------------------------------
## Variance inflation factors
## ----------------------------------------------------------------------------------------------
## VIF
## DIAMES 4.244679
## COMPES 2.182940
## NGE 3.528542
## MMG 4.277252
## ----------------------------------------------------------------------------------------------
## Eigenvalues and eigenvectors
## ----------------------------------------------------------------------------------------------
## Eigenvalues DIAMES COMPES NGE MMG
## 1 2.21731979 -0.5836962 0.09487169 0.57897124 0.5613292
## 2 1.07668055 -0.5145820 -0.13022977 -0.79140140 0.3031986
## 3 0.61697486 -0.4137466 -0.73021132 0.19470094 -0.5076383
## 4 0.08902479 -0.4725652 0.66395105 -0.02382582 -0.5790367
## ----------------------------------------------------------------------------------------------
## Variables with the largest weight in the eigenvalue of smallest magnitude
## ----------------------------------------------------------------------------------------------
## COMPES > MMG > DIAMES > NGE
## ----------------------------------------------------------------------------------------------
## Direct (diagonal) and indirect (off-diagonal) effects
## ----------------------------------------------------------------------------------------------
## DIAMES COMPES NGE MMG linear
## DIAMES -0.011682054 0.006207415 0.36690786 0.4627094 0.8241426
## COMPES -0.004499286 0.016117081 0.33829981 0.3186425 0.6685601
## NGE -0.005900382 0.007505714 0.72643393 -0.0469637 0.6810756
## MMG -0.007499726 0.007125379 -0.04733433 0.7207458 0.6730371
## ----------------------------------------------------------------------------------------------
Também é possível calcular uma análise para cada nível de um determinado fator
pcoeff4 <-
path_coeff(df_ge,
resp = MGE,
pred = c(MMG, COMPES, DIAMES, NGE),
by = ENV)
## Weak multicollinearity.
## Condition Number = 11.26
## You will probably have path coefficients close to being unbiased.
## Weak multicollinearity.
## Condition Number = 48.08
## You will probably have path coefficients close to being unbiased.
## Weak multicollinearity.
## Condition Number = 20.594
## You will probably have path coefficients close to being unbiased.
## Weak multicollinearity.
## Condition Number = 29.096
## You will probably have path coefficients close to being unbiased.
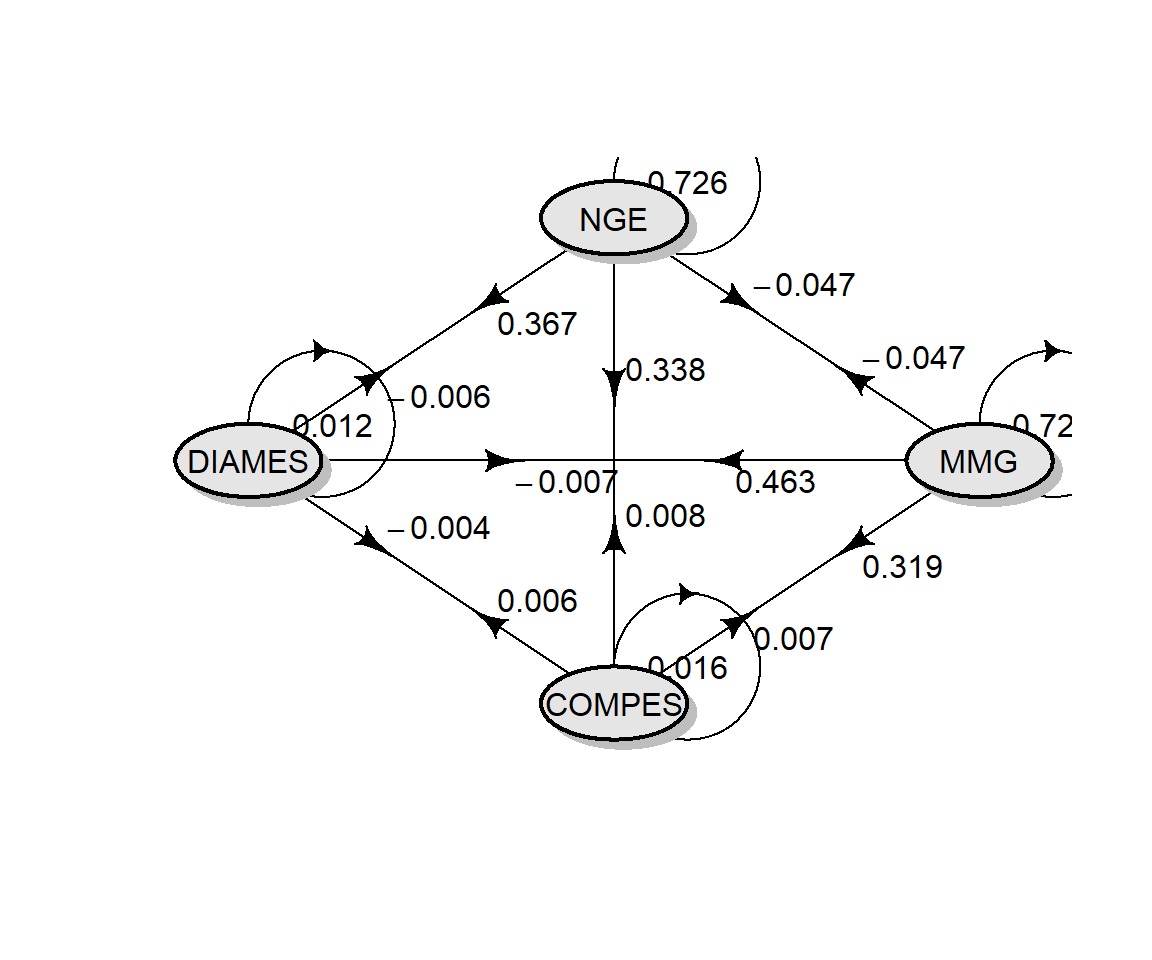
# diagrama de trilha
library(diagram)
## Carregando pacotes exigidos: shape
pcoeff5 <-
path_coeff(df_ge,
resp = MGE,
pred = c(MMG, COMPES, DIAMES, NGE))
## Weak multicollinearity.
## Condition Number = 24.907
## You will probably have path coefficients close to being unbiased.
coeffs <-
pcoeff5$Coefficients %>%
remove_cols(linear) %>%
round_cols(digits = 3)
coeffs
## MMG COMPES DIAMES NGE
## MMG 0.721 0.007 -0.007 -0.047
## COMPES 0.319 0.016 -0.004 0.338
## DIAMES 0.463 0.006 -0.012 0.367
## NGE -0.047 0.008 -0.006 0.726
plotmat(coeffs,
curve = 0,
box.size = 0.08,
box.prop = 0.5,
box.col = "gray90",
arr.type = "curved",
arr.pos = 0.35,
arr.lwd = 1,
arr.length = 0.4,
arr.width = 0.2)
Correlações canônicas
Em primeiro lugar, renomearemos as características relacionadas à planta ALT_PLANT e ALT_ESP com o sufixo _PLANTA para mostrar a usabilidade do select helper contains().
data_cc <-
df_ge %>%
rename(ESP_COMPES = COMPES,
ESP_DIAMES = DIAMES,
ESP_COMPSAB = COMP_SAB,
GRAO_MGE = MGE,
GRAO_MMG = MMG)
# Digitar os nomes das variáveis
cc1 <- can_corr(data_cc,
FG = c(GRAO_MGE, GRAO_MMG),
SG = c(ESP_COMPES, ESP_DIAMES, ESP_COMPSAB))
## ---------------------------------------------------------------------------
## Matrix (correlation/covariance) between variables of first group (FG)
## ---------------------------------------------------------------------------
## GRAO_MGE GRAO_MMG
## GRAO_MGE 1.0000000 0.6730371
## GRAO_MMG 0.6730371 1.0000000
## ---------------------------------------------------------------------------
## Collinearity within first group
## ---------------------------------------------------------------------------
## Weak multicollinearity in the matrix
## CN = 5.117
## Matrix determinant: 0.547021
## Largest correlation: GRAO_MGE x GRAO_MMG = 0.673
## Smallest correlation: GRAO_MGE x GRAO_MMG = 0.673
## Number of VIFs > 10: 0
## Number of correlations with r >= |0.8|: 0
## Variables with largest weight in the last eigenvalues:
## GRAO_MGE > GRAO_MMG
## ---------------------------------------------------------------------------
## Matrix (correlation/covariance) between variables of second group (SG)
## ---------------------------------------------------------------------------
## ESP_COMPES ESP_DIAMES ESP_COMPSAB
## ESP_COMPES 1.0000000 0.3851451 0.2554068
## ESP_DIAMES 0.3851451 1.0000000 0.6974629
## ESP_COMPSAB 0.2554068 0.6974629 1.0000000
## ---------------------------------------------------------------------------
## Collinearity within second group
## ---------------------------------------------------------------------------
## Weak multicollinearity in the matrix
## CN = 6.679
## Matrix determinant: 0.4371931
## Largest correlation: ESP_DIAMES x ESP_COMPSAB = 0.697
## Smallest correlation: ESP_COMPES x ESP_COMPSAB = 0.255
## Number of VIFs > 10: 0
## Number of correlations with r >= |0.8|: 0
## Variables with largest weight in the last eigenvalues:
## ESP_DIAMES > ESP_COMPSAB > ESP_COMPES
## ---------------------------------------------------------------------------
## Matrix (correlation/covariance) between FG and SG
## ---------------------------------------------------------------------------
## ESP_COMPES ESP_DIAMES ESP_COMPSAB
## GRAO_MGE 0.6685601 0.8241426 0.4709310
## GRAO_MMG 0.4421011 0.6419870 0.6187001
## ---------------------------------------------------------------------------
## Correlation of the canonical pairs and hypothesis testing
## ---------------------------------------------------------------------------
## Var Percent Sum Corr Lambda Chisq DF p_val
## U1V1 0.8430909 79.09135 79.09135 0.9181998 0.12194 319.84591 6 0
## U2V2 0.2228801 20.90865 100.00000 0.4721018 0.77712 38.32842 2 0
## ---------------------------------------------------------------------------
## Canonical coefficients of the first group
## ---------------------------------------------------------------------------
## U1 U2
## GRAO_MGE -0.98237574 0.9289894
## GRAO_MMG -0.02591325 -1.3518180
## ---------------------------------------------------------------------------
## Canonical coefficients of the second group
## ---------------------------------------------------------------------------
## V1 V2
## ESP_COMPES -0.4445443 0.1353212
## ESP_DIAMES -0.8650570 0.6712820
## ESP_COMPSAB 0.1955781 -1.3476588
## ---------------------------------------------------------------------------
## Canonical loads of the first group
## ---------------------------------------------------------------------------
## U1 U2
## GRAO_MGE -0.9998163 0.01916566
## GRAO_MMG -0.6870886 -0.72657362
## ---------------------------------------------------------------------------
## Canonical loads of the second group
## ---------------------------------------------------------------------------
## V1 V2
## ESP_COMPES -0.7277648 0.04966103
## ESP_DIAMES -0.8998626 -0.21654173
## ESP_COMPSAB -0.5213067 -0.84490257
# usando select helpers
cc2 <- can_corr(data_cc,
FG = contains("GRAO_"),
SG = contains("ESP_"))
## ---------------------------------------------------------------------------
## Matrix (correlation/covariance) between variables of first group (FG)
## ---------------------------------------------------------------------------
## GRAO_MGE GRAO_MMG
## GRAO_MGE 1.0000000 0.6730371
## GRAO_MMG 0.6730371 1.0000000
## ---------------------------------------------------------------------------
## Collinearity within first group
## ---------------------------------------------------------------------------
## Weak multicollinearity in the matrix
## CN = 5.117
## Matrix determinant: 0.547021
## Largest correlation: GRAO_MGE x GRAO_MMG = 0.673
## Smallest correlation: GRAO_MGE x GRAO_MMG = 0.673
## Number of VIFs > 10: 0
## Number of correlations with r >= |0.8|: 0
## Variables with largest weight in the last eigenvalues:
## GRAO_MGE > GRAO_MMG
## ---------------------------------------------------------------------------
## Matrix (correlation/covariance) between variables of second group (SG)
## ---------------------------------------------------------------------------
## ESP_COMPES ESP_DIAMES ESP_COMPSAB
## ESP_COMPES 1.0000000 0.3851451 0.2554068
## ESP_DIAMES 0.3851451 1.0000000 0.6974629
## ESP_COMPSAB 0.2554068 0.6974629 1.0000000
## ---------------------------------------------------------------------------
## Collinearity within second group
## ---------------------------------------------------------------------------
## Weak multicollinearity in the matrix
## CN = 6.679
## Matrix determinant: 0.4371931
## Largest correlation: ESP_DIAMES x ESP_COMPSAB = 0.697
## Smallest correlation: ESP_COMPES x ESP_COMPSAB = 0.255
## Number of VIFs > 10: 0
## Number of correlations with r >= |0.8|: 0
## Variables with largest weight in the last eigenvalues:
## ESP_DIAMES > ESP_COMPSAB > ESP_COMPES
## ---------------------------------------------------------------------------
## Matrix (correlation/covariance) between FG and SG
## ---------------------------------------------------------------------------
## ESP_COMPES ESP_DIAMES ESP_COMPSAB
## GRAO_MGE 0.6685601 0.8241426 0.4709310
## GRAO_MMG 0.4421011 0.6419870 0.6187001
## ---------------------------------------------------------------------------
## Correlation of the canonical pairs and hypothesis testing
## ---------------------------------------------------------------------------
## Var Percent Sum Corr Lambda Chisq DF p_val
## U1V1 0.8430909 79.09135 79.09135 0.9181998 0.12194 319.84591 6 0
## U2V2 0.2228801 20.90865 100.00000 0.4721018 0.77712 38.32842 2 0
## ---------------------------------------------------------------------------
## Canonical coefficients of the first group
## ---------------------------------------------------------------------------
## U1 U2
## GRAO_MGE -0.98237574 0.9289894
## GRAO_MMG -0.02591325 -1.3518180
## ---------------------------------------------------------------------------
## Canonical coefficients of the second group
## ---------------------------------------------------------------------------
## V1 V2
## ESP_COMPES -0.4445443 0.1353212
## ESP_DIAMES -0.8650570 0.6712820
## ESP_COMPSAB 0.1955781 -1.3476588
## ---------------------------------------------------------------------------
## Canonical loads of the first group
## ---------------------------------------------------------------------------
## U1 U2
## GRAO_MGE -0.9998163 0.01916566
## GRAO_MMG -0.6870886 -0.72657362
## ---------------------------------------------------------------------------
## Canonical loads of the second group
## ---------------------------------------------------------------------------
## V1 V2
## ESP_COMPES -0.7277648 0.04966103
## ESP_DIAMES -0.8998626 -0.21654173
## ESP_COMPSAB -0.5213067 -0.84490257
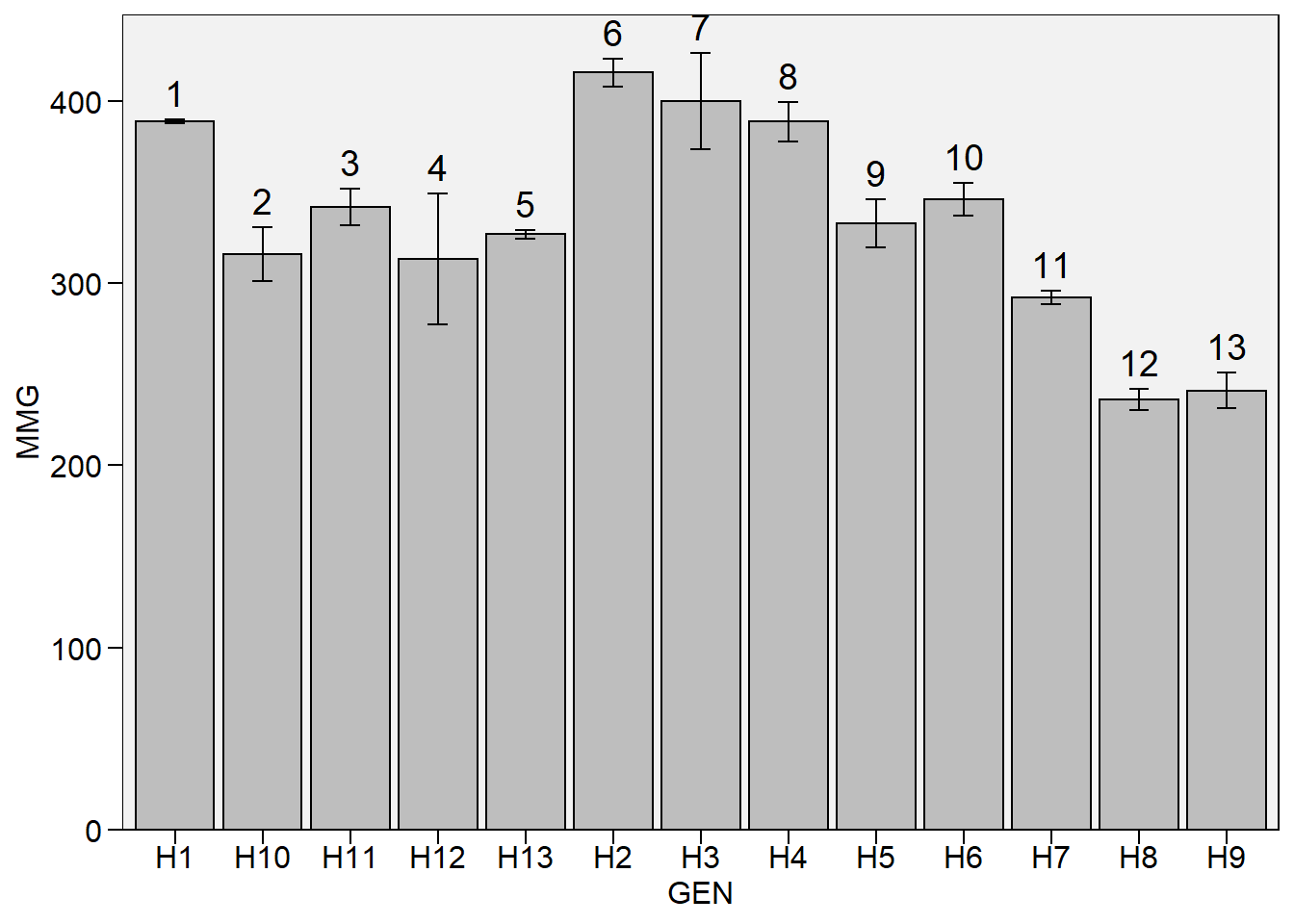
Gráfico de barras
plot_bars(df_g,
x = GEN,
y = MMG,
lab.bar = 1:13)
plot_factbars(df_ge, ENV, GEN, resp = MMG)
## Warning in RColorBrewer::brewer.pal(n, pal): n too large, allowed maximum for palette Spectral is 11
## Returning the palette you asked for with that many colors
-
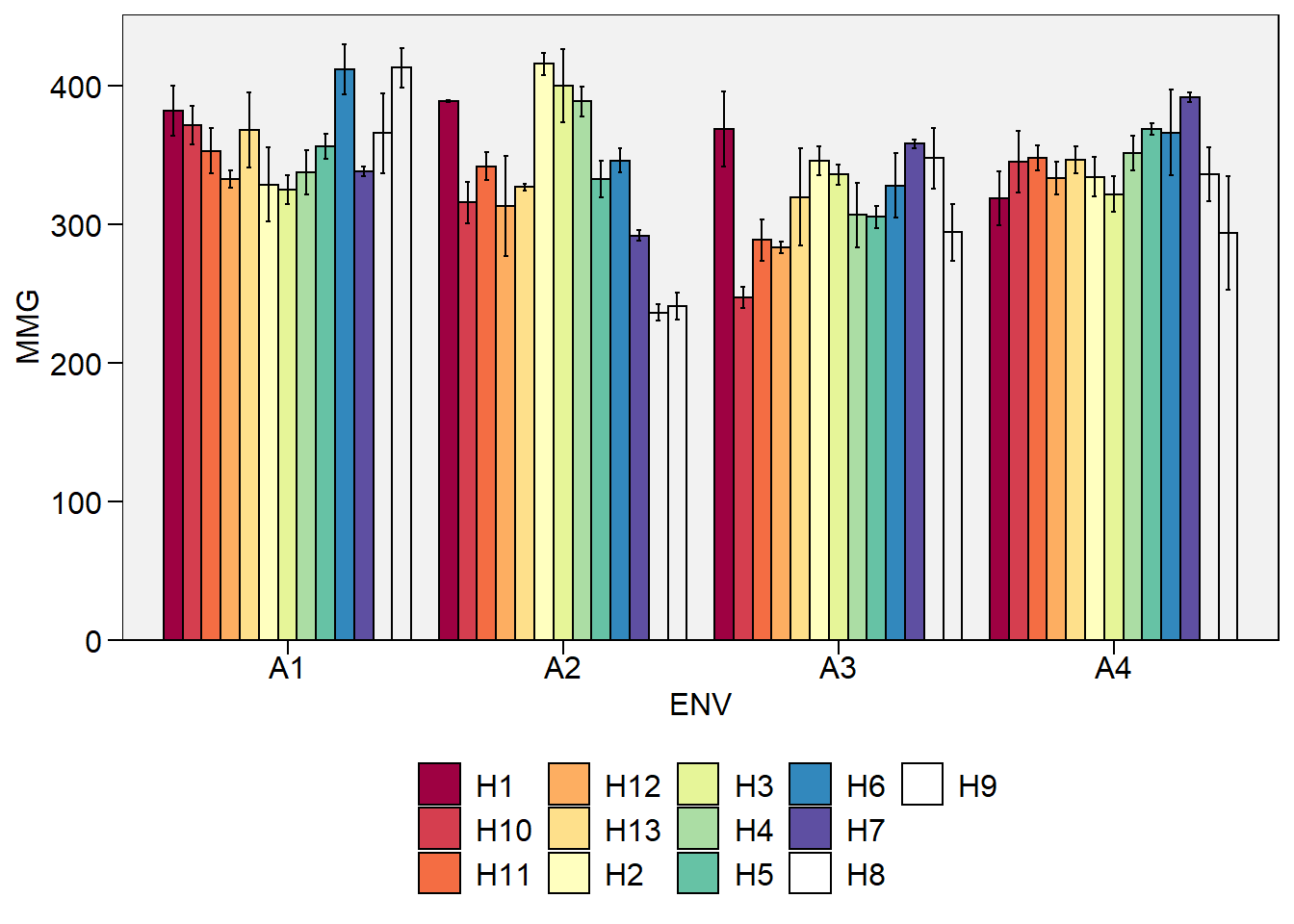
Olivoto, T., Souza, V. Q., Nardino, M., Carvalho, I. R., Ferrari, M., Pelegrin, A. J., Szareski, V. J., & Schmidt, D. (2017). Multicollinearity in path analysis: A simple method to reduce its effects. Agronomy Journal, 109(1), 131–142. https://doi.org/10.2134/agronj2016.04.0196 ↩︎